핸즈온 머신러닝
코딩관련깃허브

안녕하세요. 팀 언플(Team Unsolved Problem)에 에디터 ㅋ헬 킴(Khel Kim), 김현호입니다. 라온 피플 포스팅을 백곰 백승열 에디터가 잘 정리해서 올려주었습니다.
오늘부터는 머신러닝의 교과서로 인정받고 있는 ‘핸즈온 머신러닝’을 함께 공부하고 차례대로 정리해보도록 하겠습니다.
Chapter 1 같은 경우에는 저희가 라온 피플 포스팅에서 어느 정도 다뤘다고 생각이 되어 생략하고 Chapter 2부터 공부하도록 하겠습니다. Chapter 2는 한 프로젝트를 처음부터 끝까지 작업하는 것이기 때문에 자세히 여러 차례 나눠서 진행하도록 하겠습니다.
혹시 Chapter 1 관련해서 질문이 있으시다면 편하게 메일 주시면 됩니다.


그럼, 시작하겠습니다!


이 단원에서는 우리가 직접 데이터사이언티스트가 되어 한 프로젝트를 처음부터 끝까지 다뤄보도록 하겠습니다. 우리가 다룰 분야의 데이터는 부동산 데이터입니다!

먼저 데이터사이언티스트로서 어떤 스탭들을 밟아나갈지를 살펴보죠.

1. Look at the big picture.
   
   
2. Get the data.
   
   
3. Discover and visualize the data to gain insights.
   
   
4. Prepare the data for Machine Learning algorithms.
   
   
5. Select a model and train it.
   
   
6. Fine-tune our model.
   
   
7. Present our solution.
   
   
8. Launch, monitor, and maintain our system.
   
   

0.0 Working with Real Data

우리가 데이터를 얻을 수 있는 소스들입니다.

• Popular open data repositories:
  
  
  • UC Irvine Machine Learning Repository
    
    
  • Kaggle datasets
    
    
  • Amazon’s AWS datasets
    
    
• Meta portals(they list open repositories):
  
  
  • http://dataportals.org/
    
    
  • http://opendatamonitor.eu/
    
    
  • http://quadl.com/
    
    
• Other pages listing many popular open data repositories:
  
  
  • Wikipedia’s list of Machine Learning datasets
    
    
  • Quora.com question
    
    
  • Datasets subreddit
    
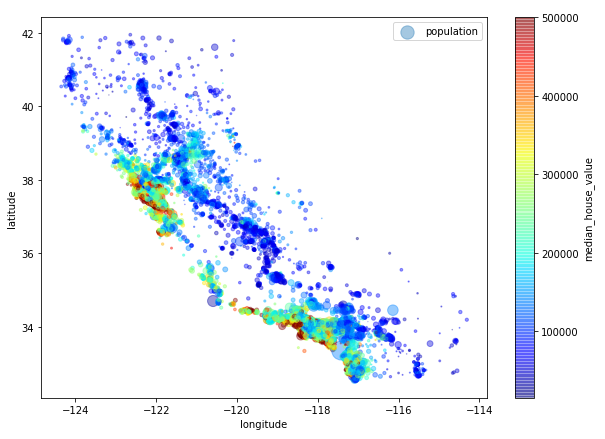
    이 단원에서는 California Housing Prices dataset from the StatLib repository를 다루겠습니다!
    
    
    
    

1.0 Look at the Big Picture

먼저 우리가 무엇을 해야하는지, 우리의 데이터는 어떻게 구성되어 있는지 체크합시다.

• Main task: 캘리포니아 데이터를 이용해서 캘리포니아 집 값을 예측하는 모델을 완성하는 것.
  
  
• 데이터: 인구수, 평균 수입, 평균 집 값 등을 특성으로 갖고 있음.
  
  

1.1 Frame the Problem

데이터를 건들기 전에 우리의 목적이 무엇인지 명확하게 규명해야 합니다. 여기서는 우리의 목적이 우리의 결과물이 또 다른 머신러닝의 데이터로 쓰인다고 가정합시다.

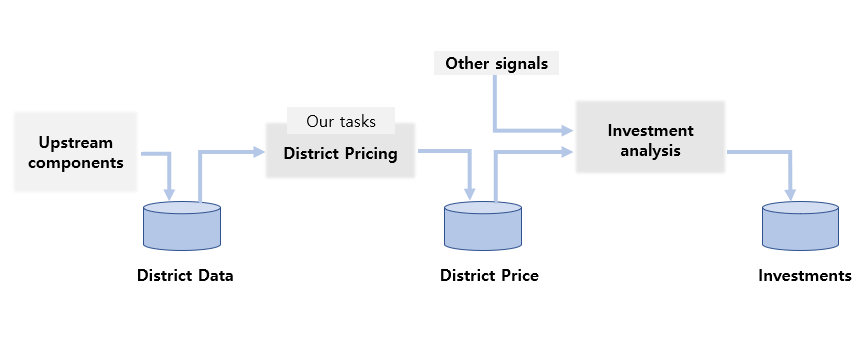
• 우리의 목적: 구역별 평균 집값의 예측이 또 다른 머신러닝 시스템에 입력되게 하는 것.
  
  
• 그리고 최종적으로는 주어진 지역에 투자하는 것이 좋을지, 좋지 않을지 결정하는데 쓰인다고 가정합시다.
  
  

우리의 목적에 따라 우리가 어떻게 이 문제를 바라볼 지, 어떤 알고리즘을 써야할지, 어떤 방식으로 우리의 모델을 평가할지, 그리고 얼마나 이 문제에 노력을 쏟을지가 결정됩니다.

• 우리는 과거에는 어떤 솔루션을 쓰는지도 알아봐야 합니다. 왜냐하면 지금 쓰고 있는 해결책들이 우리에게 문제에 대한 통찰력을 줄 수 있기 때문입니다. 하지만 지금은 과거에 있던 해결책들이 유용하지 않다고 생각해보죠(생략하겠다는 뜻입니다 ㅎㅎ).
  
  

이제 머신러닝의 관점에서 이 문제를 바라봅시다.

1. 이 학습은 지도 학습, 자율 학습, 그리고 강화 학습 중 지도 학습입니다.
   • 왜냐하면 이 학습의 데이터에는 명확한 정답이 데이터에 있기 때문입니다.
     
     
2. 이 학습은 분류 혹은 회귀 중 회귀입니다.
   • 왜냐하면 우리는 정확한 값을 내는 모델을 원하기 때문입니다.
     
     
3. 이 학습은 배치 학습과 온라인 학습 중 배치 학습을 해야 합니다.
   • 왜냐하면 이 데이터는 계속 업데이트되지 않고, 빠르게 데이터를 조정해줄 필요가 없으며, 데이터의 양 자체도 메모리에 들어갈 만큼 충분히 작기 때문입니다.
     
     

1.2 Select a Performance Measure

이제 학습 결과를 어떻게 평가할지 결정해야 합니다. 보통은 RMSE(Root Mean Square Error) 방법을 주로 사용합니다. RMSE는 에러의 표준편차를 측정합니다.

$RMSE(X, h) = (\frac{1}{m}\sum^m_{i=1}(h(x^{(i)}) - y^{(i)})^2)^{\frac{1}{2}}$

• 여기서 $m$은 데이터의 개수고, $x^{i}$는 $i$번 째 데이터 벡터(특성 값들이 각 원소인 벡터)이고, $y^{i}$는 $i$번 째 데이터의 label입니다. 또, $X$는 모든 데이터의 특성값들을 원소로 갖는 행렬이고, $h$는 우리의 예측 함수입니다.
  
  
  
  • ex)
    \(x^{(1)}=\begin{pmatrix} 1 \\ 10 \\ 100 \\ 1000 \end{pmatrix}\)
    \(y^{(i)} = 200\)
    
    \(X = \begin{pmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ \vdots \\ (x^{(1999)})^T \\ (x^{(2000)})^T \end{pmatrix} =\begin{pmatrix} 1 & 10 & 100 & 1000 \\ \vdots & \vdots & \vdots & \vdots \end{pmatrix}\)
    
    
• 아까 말씀드린 것처럼 우리는 여러가지 방법으로 학습 결과를 평가할 수 있습니다.
• MAE(Mean Absolute Error)
  $ MAE(X, h) = \frac{1}{m}\sum^m_{i = 1}|h(x^{(i)}) - y{(i)}|$
• l_k norm 등등이 있습니다.
  

$\| v \|_{k} = (|\nu_0|^k + |\nu_1|^k +\cdots + |\nu_n|^k)^\frac{1}{k} $

• 참고로 norm index(여기선 k)가 클수록, 큰 값에 영향을 많이 받고 작은 값에 영향을 덜 받습니다.
  
• 데이터에 큰 값이 많이 있지 않을 때는 RMSE가 꽤 좋은 평가 방법이고 자주 쓰입니다.
  
  

1.3 Check the Assumptions

마지막으로 이제까지 가정한 가정들을 체크해야 합니다. 왜냐하면 나중에 일어날 수 있는 심각한 문제를 일찍 확인할 수도 있기 때문입니다.

무슨 일을 하더라도 이런 식으로 큰 그림을 보고 전략을 세우는 일은 언제나 중요하죠. 다음 포스팅에는 실제 데이터를 코드와 함께 살펴볼 수 있도록 하겠습니다.