핸즈온 머신러닝
코딩관련깃허브
안녕하세요. 팀 언플(Team Unsolved Problem)에 에디터 ㅋ헬 킴(Khel Kim), 김현호입니다.
오늘은 지난 시간 Chapter 2. End-to-End Machine Learning Landscape에 이어서 Chapter 3. 분류에 들어가겠습니다. 너무나 감사드리게도 저희에게 후원이 들어와서 저희도 한글책을 갖게 되었습니다!! 오늘부터는 챕터 제목도 한글로 갑니다!
[Hands-on ML] Chapter 2. End-to-End Machine Learning Project6
그럼, 시작하겠습니다!
기본설정
import numpy as np ##배열, 3장에서는 DataFrame은 다루지 않음
import os ##사실 3장에서는 필요 없음
import matplotlib ##그림용
import matplotlib.pyplot as plt ##그림용
import sklearn ##사이킷런
np.random.seed(42) ##랜덤시드
matplotlib.rc('font', family='NanumBarunGothic') ##matplotlib 한글을 위해
plt.rcParams['axes.unicode_minus'] = False ##한글을 위해
3.0 Introduction
3.1 MNIST
3.2 이진 분류기 훈련
3.3 성능 측정
3.4 다중 분류
3.5 에러 분석
3.6 다중 레이블 분류
3.7 다중 출력 분류
가장 일반적인 지도 학습 작업은 회귀(값 예측)와 분류(클래스 예측)입니다. 저희는 2장에서는 주택 가격을 예측하는 회귀 작업을 했고, 선형 회귀, 결정 트리, 랜덤 포레스트 알고리즘을 보았습니다. 이제 3장에서는 분류 시스템을 집중적으로 다뤄보겠습니다.
이 장에서는 숫자 이미지를 모은 MNIST 데이터셋을 사용하겠습니다.
from sklearn.datasets import fetch_openml ##책과 다름. 유의
mnist = fetch_openml('mnist_784', version=1) ##mnist는 Bunch라는 자료구조
X, y = mnist["data"], mnist["target"] ##numpy의 배열로 저장
y = y.astype(np.int) ##mnist의 target이라는 key안에는 value가 문자열로 저장되어 있음. int로 바꿔줘야함.
###읭스럽게도 4번 돌리면 home/scikit_learn_datasets/~/opemml.org에 data가 생김
저는 어떻게 돌아가는 매커니즘인지 모르겠는데, 이 코드를 세 번째까지는 돌릴 때마다 오류가 발생하다가, 4 번째에 데이터가 생깁니다. 어떻게 이러는지 모르겠네요…;;;
참고로 Bunch와 dictionary는 상당히 비슷한 자료형태입니다. 하지만 Bunch와 dictionary와의 차이는 Bunch 자료형은 value를 부를 때, DATA.KEY라는 식으로도 value를 부를 수 있습니다.
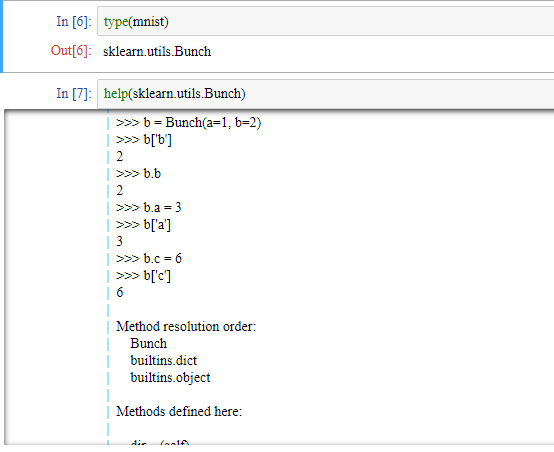
데이터 개수를 관찰해 보죠.
X.shape ## 결과 (70000, 784)
y.shape ## 결과 (70000,)
저희의 데이터의 개수는 70000개입니다. 부동산 데이터보다는 많군요 ㅎ.
데이터 하나를 잡아서 그려봅시다.
some_digit_9 = X[36000]
some_digit_9_image = some_digit_9.reshape(28, 28) ### image 픽셀의 형태대로 shape를 만듦
plt.imshow(some_digit_9_image, cmap = matplotlib.cm.binary,
interpolation="bilinear")
###matplotlib.cm.binary: 색 입히는 방식.색을 흰색에서부터 검은색으로 칠해줌
###interpolation의 default값이 nearest임
plt.axis("off")
plt.show()

제 생각에는 9처럼 보이는데 실제로도 9인지 확인해 봅시다.
y[36000] ## 결과 9
제 생각이 맞았습니다. 저는 훈련이 잘된 분류기입니다. ㅋㅋㅋㅋㅋ
각설하고, 다시 내용으로 들어가면 원래는 훈련 세트와 테스트 세트를 2장에서 했던 것처럼 나눠야 합니다. 하지만 MNIST 데이터는 (특별하게) 이미 나눠져있습니다.
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
아마 핸즈온 개정 전 데이터셋은 훈련 세트에 데이터가 순서대로 되어있었나 봅니다. 하지만 저희 데이터는 이미 순서가 섞여있습니다. 그래도 재미삼아 순서를 섞어보죠.
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
저희는 아직 레벨이 낮기 때문에 이 섹션에서는 이진 분류만 해보겠습니다. 다시 말해 이 섹션에서는 주어진 데이터를 5인 데이터와 5가 아닌 데이터로 분류하는 모델을 만들겠습니다.
일단 데이터 셋과 테스트 셋에서 target이 5인 객체들을 알아봅시다.
y_train_5 = (y_train == 5) ##bool 값으로 나옴
y_test_5 = (y_test == 5)
이제 분류 모델을 하나 선택해서 훈련시키겠습니다. 사이킷런의 SGDClassifier 클래스를 사용해 확률적 경사 하강법(SGD) 분류기를 사용해보겠습니다.
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter=5, random_state=42) ##4단원에서 자세히 하겠습니다.
sgd_clf.fit(X_train, y_train_5) ##fit 메소드를 사용, 각 객체 변수에 특정 값들을 저장.
sgd_clf.predict([some_digit_9, X[1]]) ##some_digit_9은 (1, 784) 배열
##some_digit_9이 5인가 ==> false
우리의 분류기는 X[36000]과 X[1]은 5가 아니라고 답하는군요!
분류기 평가는 회귀 모델 평가보다 훨씬 어렵습니다. 이유는 밑에 섹션에서 알려드리겠습니다. 사용할 수 있는 성능 지표도 많이 있습니다.
이번 섹션에서는 교차 검증을 통해 정확도를 측정해보겠습니다. 가끔은 사이킷런이 제공하는 기능보다 교차 검증 과정을 더 많이 제어해야 할 필요가 있습니다. 그래서 같은 작업을 하는 코드를 직접 구현해 보겠습니다.
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42) ###랜덤 시드 42로 총 3번 train set과 test set을 나눔
for train_index, test_index in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf) ###sgd_clf의 clone을 만듦
X_train_folds = X_train[train_index]
y_train_folds = (y_train_5[train_index])
X_test_fold = X_train[test_index]
y_test_fold = (y_train_5[test_index])
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold) ##bool 값을 sum하면 true의 개수가 나옴. 사실 파이썬에서 True=1, False=0
print(n_correct / len(y_pred)) ## scoring =' accuracy'
#결과
0.9605
0.95595
0.95375
혹시 코드에 대해 질문이 있으시면 댓글이나 메일 보내시면 대답해드리겠습니다.
사이킷런의 내장함수를 이용해 교차 검증 해보겠습니다.
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring='accuracy')
## scoring ='acuracy' 는 맞은 개수 나누기 전체 개수
#결과
array([0.9605 , 0.95595, 0.95375])
무려 정확도 95% 성능을 내는 분류기를 만들었습니다. 하지만 여기엔 트릭이 숨어있습니다. 왜냐면 샘플 개수의 차이가 많이나는 분류기에서 교차 검증은 효과적이지 못하기 때문입니다(만약 데이터가 5가 10개, 5가 아닌 것이 90개인 샘플들로 구성되어있으면, 모든 샘플에게 5가 아니라고 말하는 분류기의 정확도는 90%입니다). 예를 들어 모든 것을 5가 아니라고 말하는 분류기를 만들어서 교차검증을 해보죠.
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None): ##cross_val_score에 들어가려면 필요함
pass
def predict(self, X):
return np.zeros((len(X),1), dtype=bool)
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")
###cross_val_score 안에 자동으로 fit 매소드와 .predict 객체변수를 불러오는 듯
#결과
array([0.909 , 0.90745, 0.9125 ])
무려 정확도가 90%이군요… 이런 식으로 클래스별 샘플 개수가 많이 차이나는 데이터셋을 분류할 때, 교차 검증은 효과적이지 못합니다.
이렇게 샘플의 개수가 많이 차이나는 경우 교차 검증말고 다른 지표를 사용해야 합니다. 그 중 하나가 오차 행렬을 조사하는 것입니다.
일단 우리 모델이 우리의 훈련 세트를 어떻게 예측했는지 살펴보겠습니다.
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
## cv=3이니깐 데이터 셋을 1,2,3으로 나누고
## 1,2로 3을 예측 & 1,3으로 2를 예측 $ 2,3으로 1을 예측하고
## 우측에 있는 예측 값들을 반환함
이 예측을 바탕으로 오차 행렬을 만들어 봅시다.
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
#결과
array([[52972, 1607],
[ 989, 4432]], dtype=int64)
이 오차 행렬을 분석해보면,
라는 뜻입니다. 오차 행렬을 말로 설명하려면 어려우니 예제부터 봤습니다. 표로 한 번 더 보시죠.
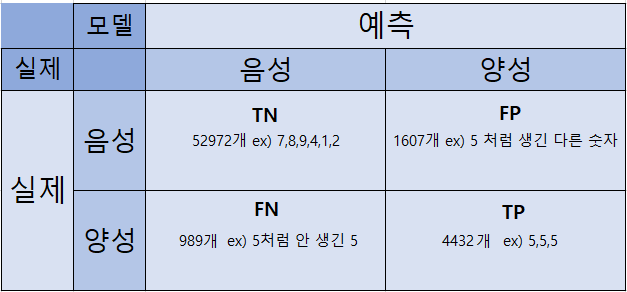
오차행렬에 대한 감이 오시나요? 이 오차 행렬을 보면 이 분류기가 제대로 분석한 것 얼마나 되는 지 알 수 있습니다. 하지만 아직 어떻게 교차 검증의 한계를 뛰어넘을지 알려드리지 않았습니다. 교차 검증의 한계를 뛰어넘을 수 있는 새로운 지표를 정의하겠습니다.
이런 비율을 정의함으로서 저희는 각 클래스에 객체수에 상관없이 모델의 성능을 측정할 수 있습니다.
이 지표들이 어떤 차이를 갖는지는 다음 섹션에서 관찰하겠습니다.
사이킷런에 정밀도와 재현율을 구하는 함수가 있습니다.
from sklearn.metrics import precision_score, recall_score
print (precision_score(y_train_5, y_train_pred))
print (recall_score(y_train_5, y_train_pred))
# 결과
0.7338963404537175
0.8175613355469471
또 다른 지표가 있는데 F1 점수라고 합니다.
정밀도와 재현율이 비슷한 분류기에서는 F1 점수가 높습니다. 하지만 상황에 따라 정밀도가 중요한 상황과 재현율이 중요한 상황이 있습니다.
사이킷런에 F1 점수를 구하는 함수가 있습니다.
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
#결과
0.7734729493891798
정밀도와 재현율에 대해 자세히 살펴보죠. 모델을 훈련 시키면 모델은 각 데이터에게 점수를 줍니다. 밑에 그림을 보면 각 점수가 1, 10, 20, 30, 40, 50, 60, 70 입니다. 이때 이 점수가 결정 임곗값(threshold)을 넘으면 양성, 넘지 않으면 음성입니다.
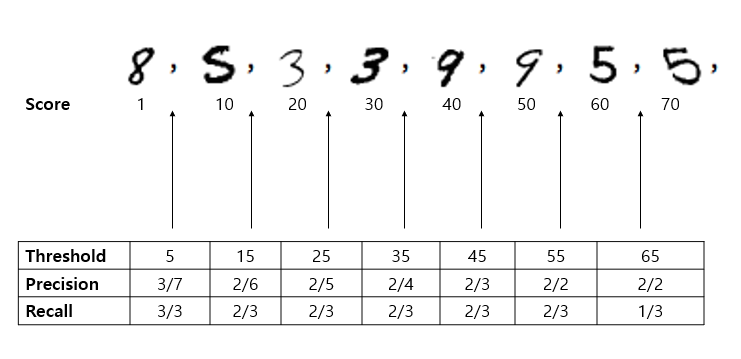
여기서 중요한게 결정 임곗값에 따라 정밀도와 재현율이 달라집니다. 그림에서 볼 수 있듯이 임곗값이 올라갈 수록 정밀도는 커지고 재현율은 줄어듭니다.
가장 기초적으로는 임곗값이 올라가면 FP가 감소하고 FN이 증가합니다.
이해가 쉽도록 몇 가지 성질을 말해보겠습니다.
좀 더 나아가서 말로 풀어보겠습니다.
결과적으로 두 지표는 트레이드 오프 관계입니다. 상황에 따라 정밀도가 중요한 상황과 재현율이 중요한 상황이 있습니다.
적절한 임곗값을 구하기 위해 모든 샘플의 점수를 구해봅시다.
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
method="decision_function")
##어떤 식으로 scoring을 계산하는지는 모릅니다.
##나중에 4단원에서 안나오면 다시 공부할 것입니다.
이 점수로 precision_recall_curve() 함수를 사용해서 가능한 임곗값에 대해 정밀도와 재현율 그래프를 그릴 수 있습니다.
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
여기서 제 사적인 궁금증이 생겼었습니다. 일단 그림을 보시죠.
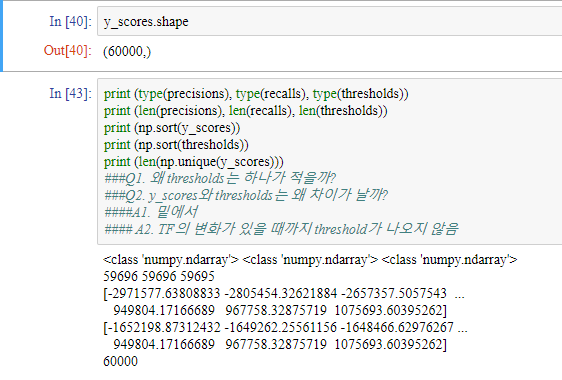
Q2는 쉽게 알 수 있지만, Q1은 왜인지 알기가 어려웠습니다. 하지만 열심히 탐구해서 정답 비슷한걸 알게 된 것 같아서 여기에 적겠습니다. ㅎㅎ
threshold가 매우 크다면
threshold가 매우 작다면

이제 맷플롭립을 이용해 정밀도와 재현율 함수를 그려보겠습니다.
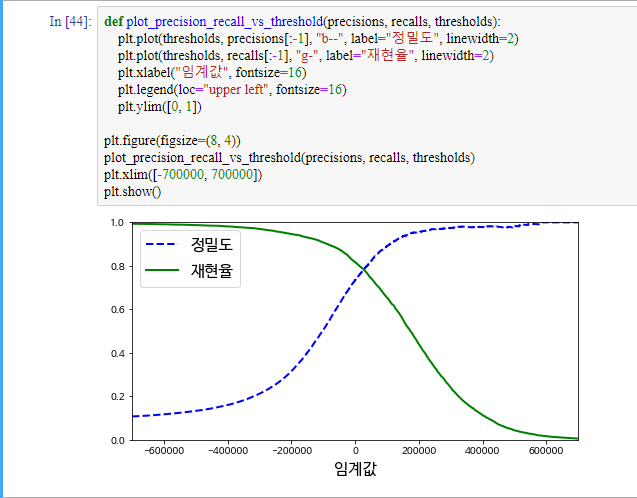
정밀도 곡선이 재현율 곡선보다 왜 더 울퉁불퉁한지도 위에 설명을 잘 이해하셨다면 이해하실 수 있습니다.
재현율에 대한 정밀도 곡선을 그리면 좋은 정밀도/재현율 트레이드오프를 선택할 수 있습니다.
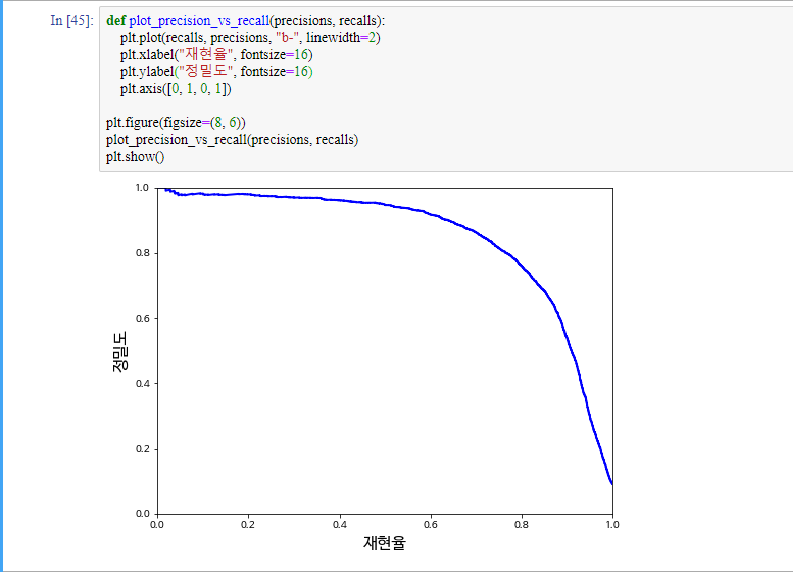
만약 정밀도 90%가 목표라고 합시다.
y_train_pred_90 = (y_scores > 70000) ##대충보고... 임계값을 설정
print(precision_score(y_train_5, y_train_pred_90)) #정밀도 계산
print(recall_score(y_train_5, y_train_pred_90)) #재현율 계산
#결과
0.855198572066042
0.7070651171370596
우리는 분류기를 만들 때, 정밀도와 재현율을 상대적으로 비교해서 분류기를 만들어야합니다. 누군가가 ‘99% 정밀도를 달성하자’라고 말하면 반드시 ‘재현율 얼마에서?’라고 물어야합니다.
이번 섹션에서는 이진 분류 모델의 지표 중 하나인 ROC(receiver operating characteristic)를 배워보도록 하겠습니다. 거짓 양성 비율(FPR)에 대한 진짜 양성 비율(TPR, 재연율의 다른 이름)입니다.
from sklearn.metrics import roc_curve
fpr, tpr, threshold = roc_curve(y_train_5, y_scores)
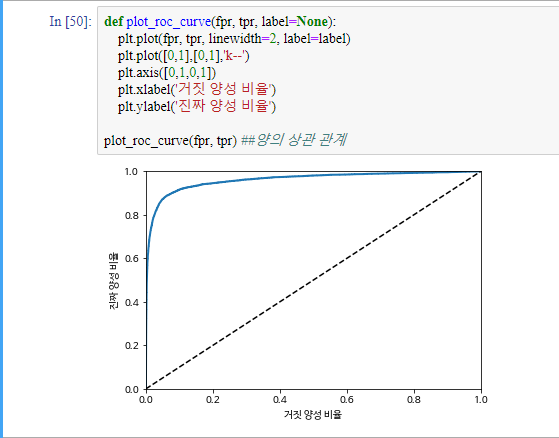
거짓 양성 비율도 진짜 양성 비율(재현율)과 트레이드오프 관계가 있습니다. 좋은 분류기는 y=x 그래프와 ROC 곡선이 최대한 멀리 떨어져 있어야 합니다. 곡선 아래의 면적을 새로운 지표로 생각하고 이를 통해 분류기들을 비교할 수 있습니다. 이를 AUC(area under the curve) 측정 이라고 합니다.
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
#결과
0.9614189997126434
RandomForestClassifier와 SGDClassifier를 비교해보겠습니다
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(n_estimators=10, random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
method="predict_proba")
y_scores_forest = y_probas_forest[:, 1] ## 5 클래스에 들어갈 확률을 점수로 사용
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
## y_train_5는 bool 값을 가지고 있는 배열
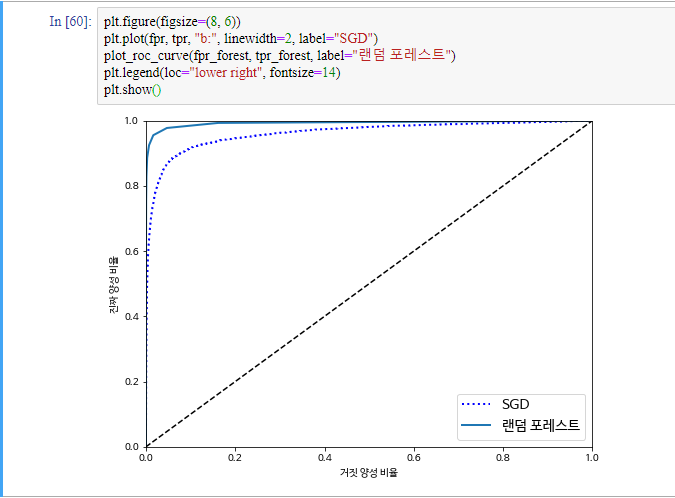
roc_auc_score(y_train_5, y_scores_forest)
0.9928250745111685
이것으로 RandomForestClassifier가 SGDClassifier보다 좋은 것을 알 수 있습니다. 추가로 정밀도와 재현율을 구해보겠습니다.
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
precision_score(y_train_5, y_train_pred_forest)
#결과
0.9870386643233744
recall_score(y_train_5, y_train_pred_forest)
#결과
0.8288138719793396
이진 분류가 두 개의 클래스를 구별한다면 다중 분류기는 둘 이상의 클래스를 구별할 수 있습니다. 하지만 일부 알고리즘은 여러 개의 클래스를 직접 처리할 수 있지만, 몇 몇 알고리즘은 이진 분류만 가능합니다. 그럼에도 불구하고 이진 분류기를 여러 개 이용해 다중 클래스를 분류하는 기법도 있습니다.
SGDClassifier 훈련
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit_9])
#결과
array([4]) ##틀렸네요 ㅋㅋㅋ
이는 10개의 분류기를 통과하면서 점수가 가장 높은 클래스를 선택한 것입니다.
some_digit_9_scores = sgd_clf.decision_function([some_digit_9])
some_digit_9_scores
#결과
array([[-736165.13534356, -391182.59305387, -752094.90919363,
-199593.6564959 , -33428.88555026, -176288.21703149,
-856742.40238951, -145757.71304016, -253587.97052021,
-249064.39096412]])
np.argmax(some_digit_9_scores)
4
sgd_clf.classes_
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
보통은 sgd_clf.classes_[4]가 어떤건지 직관적으로 알기 어렵습니다.
OvO나 OvA를 강제로 선택해 줄 수 있습니다.
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(max_iter=5, random_state=42))
ovo_clf.fit(X_train, y_train) ##fit 매소드를 실행하면서 여러가지 객체 변수에 값을 집어넣음.
ovo_clf.predict([some_digit_9])
#결과
array([9]) ## 맞았습니다!!
len(ovo_clf.estimators_) ##분류기 개수
#결과
45
RandomForestClassifier 훈련
forest_clf.fit(X_train, y_train)
forest_clf.predict([some_digit_9])
#결과
array([9])
분류기가 추정하는 정도
forest_clf.predict_proba([some_digit_9, X_train[10]])
#결과
array([[0. , 0. , 0. , 0. , 0.1, 0. , 0. , 0. , 0. , 0.9],
[0. , 0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ]])
분류기의 교차 검증
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring= 'accuracy')
#결과
array([0.81908618, 0.86379319, 0.84492674])
분류기에서도 scale조정을 해주면 추정값이 좋아집니다.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring ='accuracy')
#결과
array([0.91131774, 0.90884544, 0.90883633])
원칙적으로는
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3) ### 예상 값들을 출력
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
#결과
array([[5730, 2, 22, 9, 11, 52, 47, 8, 39, 3],
[ 1, 6459, 54, 29, 6, 43, 6, 11, 123, 10],
[ 53, 34, 5371, 90, 80, 23, 79, 57, 157, 14],
[ 48, 37, 147, 5315, 3, 248, 36, 58, 143, 96],
[ 20, 25, 45, 10, 5338, 10, 49, 36, 87, 222],
[ 72, 40, 38, 170, 72, 4616, 108, 28, 186, 91],
[ 35, 24, 56, 1, 39, 86, 5622, 6, 49, 0],
[ 22, 20, 73, 28, 48, 12, 4, 5832, 18, 208],
[ 53, 146, 84, 152, 14, 147, 55, 27, 5037, 136],
[ 44, 33, 29, 89, 164, 39, 3, 211, 77, 5260]],
dtype=int64)
행은 실제 값이고 열은 추정값입니다. 하지만 이렇게 보면 직관적으로 파악하기 어렵습니다.

지금은 샘플의 절대 개수에 따라 명도가 정해져서 샘플의 상대적 개수를 파악하기 어렵습니다. 조금 조작을 해보겠습니다.
row_sums = conf_mx.sum(axis=1, keepdims=True) ##keepdims는 밑에서...
norm_conf_mx = conf_mx / row_sums
keepdims에 대해 잠시만 알아보겠습니다
a = np.array([[1,2,3],[4,5,6],[7,8,9]])
a.sum(axis=1) ### 2에서 1로 dim이 떨어짐
#결과
array([ 6, 15, 24])
a.sum(axis=1, keepdims=True) ### column을 유지하고 dim도 유지
#결과
array([[ 6],
[15],
[24]])
a.sum(axis= 0, keepdims= True) ### row를 유지하고 dim도 유지
#결과
array([[12, 15, 18]])
a.sum(keepdims=True) ### dim 유지
#결과
array([[45]])
다시 복귀
가운데를 0으로 만들고 다시 관찰해보겠습니다(오차 부분의 색 대조 만들겠습니다).

개개의 에러 분석을 해볼 수 있지만 분류기가 무슨 일을 하고, 왜 잘못되었는지에 대해 통찰을 얻을 수 있지만, 더 어렵고 시간이 오래 걸립니다.
우리의 분류기의 오차 행렬을 관찰했을 때, 우리의 분류기는 3과 5를 많이 헷갈려합니다. 이 개개의 에러를 분석하기 위해 3과 5의 샘플을 그려보겠습니다.
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = matplotlib.cm.binary, **options)
plt.axis("off")
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()

분류를 하다보면 한 샘플이 여러 클래스에 속할 때가 있습니다. 이를 위해 다중 레이블 분류 시스템을 사용해야합니다. 이를 위한 분류기 중 KNeighborsClassifier가 있습니다.
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
some_digit_9에 대해 잘 추정하는지 확인하겠습니다.
knn_clf.predict([some_digit_9])
#결과
array([[ True, True]])
잘하네요! ㅎㅎ
노이즈가 들어간 샘플을 만들어 보겠습니다.
noise = np.random.randint(0,100, (len(X_train),784)) # 훈련 세트를 위한 노이즈
X_train_mod = X_train + noise
noise = np.random.randint(0,100, (len(X_test),784)) # 테스트 세트를 위한 노이즈
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
노이즈가 들어간 샘플을 그려보겠습니다.
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = matplotlib.cm.binary,
interpolation="nearest")
plt.axis("off")
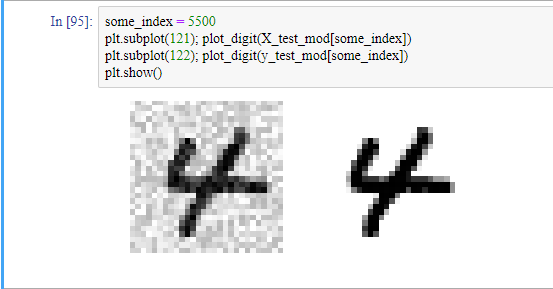
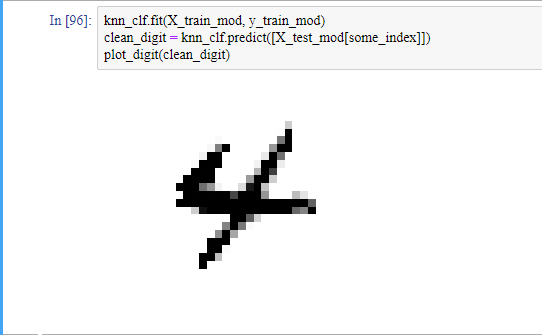
샘플들을 훈련 시키고, 노이즈가 들어간 샘플을 모델에 넣으면, 알고리즘이 샘플의 값(픽셀)들을 추정하고 출력합니다(다중 출력).
저희는 2단원에서 회귀 하는 방법을 배우고 3단원에서는 분류를 하는 방법을 배웠습니다. 다음 단원부터는 모델 하나하나를 뜯어서 살펴보도록 하겠습니다.