코딩관련깃허브
Author : Duck Hyeun, Ryu
안녕하세요. 팀 언플(Team Unsolved Problem)의 또다른 에디터인 Polar B 입니다! 오늘 포스팅할 것은 핸즈온 머신러닝의 4장, Training Models, 입니다. 팀 일원인 Duck군의 글을 정리해서 다시 업데이트하는 글이 되겠습니다!
오늘은 지난 시간 ‘Chapter 3. 분류’에 이어서 ‘Chapter 4. 모델 훈련’에 들어가겠습니다.
[Hands-On ML] Chapter 3. Classification
그럼, 출발해볼까요?!
이번 포스트에서는 4.4 학습 곡선까지만 다룰 예정입니다.
앞장과는 달리 이제는 실제 모델과 훈련 알고리즘이 어떻게 작동하는지 살펴볼 것입니다. 가장 간단한 모델 중 하나인 선형 회귀부터 시작해서 다항 회귀를 살펴보고 모델 학습에서 발생할 수 있는 과대적합 문제를 해결할 수 있는 규제 기법을 알아보겠습니다. 끝으로 분류에 널리 쓰이는 로지스틱 회귀와 소프트맥스 회귀를 알아보겠습니다.
선형 회귀(Linear Regression)는 종속변수 y와 한 개 이상의 독립 변수(또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법입니다.
선형 모델의 예측
\(\hat{y} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n\)
선형 모델의 예측 벡터형태
\(\hat{y} = h_{\theta}(x) = \theta^T \cdot x\)
위의 식이 바로 선형 회귀 모델입니다. 이제 훈련을 시켜야겠죠? 모델을 훈련시킨다는 뜻은 모델이 훈련세트에 가장 잘 맞도록 모델 파라미터를 설정하는 것입니다. 그러기 위해선 모델의 예측값이 얼마나 실제 타겟값과 비슷한 지(즉, 모델의 성능이 얼마나 좋은 지) 알 수 있어야합니다.
그것을 알게 해주는 것이 바로 회귀에서 가장 널리 쓰이는 성능 측정 지표인 평균 제곱근 오차(RMSE) 입니다(2장을 다루는 포스터 중 첫번째 포스트를 확인해보시기 바랍니다). 따라서 선형 회귀 모델을 훈련시킨다는 뜻은 RMSE를 최소화하는 $\theta$를 찾아낸다는 것입니다. RMSE와 평균 제곱 오차(Mean square error, MSE)는 최소화하는 것이 같은 결과는 내지면서 더 간단합니다. 따라서 우리는 MSE를 쓰도록 하겠습니다.
평균 제곱 오차 비용함수(Mean square error cost function)
\(MSE(X,h_\theta) = \frac{1}{m} \sum_{i=1}^{m} (\theta^T \cdot x_i - y_i)^2\)
방금 보았던 비용 함수를 최소화하는 $\theta$값을 찾는 식이 있습니다. 바로 정규 방정식입니다.
정규방정식(Normal equation)
\(\hat{\theta} = (X^T \cdot X)^{-1} \cdot X^T \cdot y\)
위 공식을 테스트해보죠! 선형적인 모습을 한 데이터를 만들겠습니다.
## 100개의 변수 생성
import numpy as np
X = 2 * np.random.rand(100,1) ## 100X1의 의 배열로 무작위 숫자를 생성
y = 4 + 3 * X+np.random.randn(100,1) ## 약간의 노이즈를 섞은 일차함수
## rand는 rand 명령은 0부터 1사이에서 균일한 확률 분포로 실수 난수를 생성
## randn은 정규확률분포(Standard normal distribution)를 따르는 난수를 생성
이것을 matplotlib을 이용해서 그래프로 표현해보면…
import matplotlib.pyplot as plt
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()
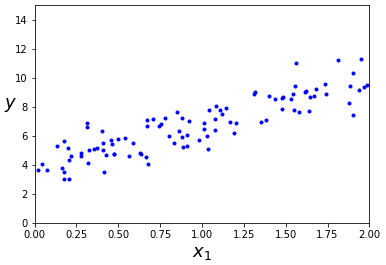
그럴싸 하쥬?
이제 여기서 정규방정식을 사용해서 $\hat{\theta}$를 계산해봅시다.
x_b = np.c_[np.ones((100,1)),X] ## 모든 샘플에 X0 = 1을 추가함
theta_best = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y) ## 정규방정식 코드구현
결과는?!

우리가 사용한 함수는 $y = 3x + 4 + 노이즈$ 였습니다. 따라서 우리는 $\theta_0 = 4, \theta_1 = 3$이 나오기를 원했지만, 실제로는 $\theta_0 = 3.80162531, \theta_1 = 3.04060515$가 나왔습니다. 노이즈 때문에 근사하긴 하지만 정확한 값은 나오지 않습니다.
그럼 이 새로운 $\hat{\theta}$(=theta_best)를 사용해서 예측을 해보겠습니다.
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2,1)), X_new] ## 모든 샘플에 x0 = 1을 추가함
y_predict = X_new_b.dot(theta_best) ## 훈련된 θ로 y를 예측하자
y_predict
## 결과
array([[3.80162531],
[9.8828356]])
그럼 이 모델의 예측을 그래프에 그려보도록 하겠습니다.
plt.plot(X_new, y_predict, "r-", linewidth=2, label='prediction')
## 예측된 두개의 점을 빨간색 선으로 잇는다, 선의 굵기는 2, 범례는 'prediction'
plt.plot(X, y, "b.") ## X와 y에 해당 되는 점에 파란색 점을 찍음
plt.xlabel("$x_1$", fontsize=18) ## x축 밑에 이름은 x1으로 하고 size는 18
plt.ylabel("$y$", rotation=0, fontsize=18)
## y축 왼쪽에 이름은 y로 하고 회전시키지 말고 글자크기는 18
plt.legend(loc="upper left", fontsize=14) ## prediction의 위치를 왼쪽 위로 하고 크기는 14
plt.axis([0, 2, 0, 15]) ## x축의 크기를 0에서2 , y축의 크기는 0에서 15
plt.show()
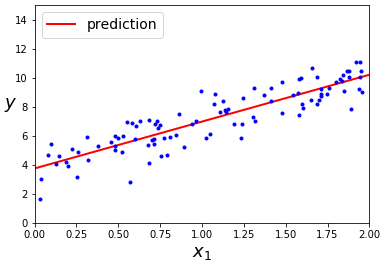
이 작업을 해주는 사이킷런의 코드가 있습니다.
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_

계산 복잡도는 일반적으로 컴퓨터가 주어진 식(혹은 코드)을 처리하는 속도와 처리할 때의 메모리 사용량를 의미합니다. 전자를 시간 복잡도, 후자를 공간 복잡도라고 합니다. 여러 표기 법이 있지만 여기서는 일반적으로 사용하는 빅오 표기법(Big-O notation)를 간단히 알아보도록 하겠습니다.
알고리즘의 소요시간이 입력의 크기의 n에 대해 $O(n^2)$이라면 최대 $n^2$에 비례하는 시간이 소요됩니다. 수학적으로 표현하자면 $Ο(g(n))$은 점근적 증가율이 $g(n)$을 넘지 않는 모든 함수의 집합입니다.
\(O(g(n)) = \{f(n) : there\;exist\;positive\;constants\;c\;and\;n_0\)
\(\qquad such\;that\;0 \leq f(n) \leq cg(n)\; for\;all\;n \geq n_0 \}\)
예를 들면
우리가 위에서 구현한 정규방정식은 크기가 $(n+1) \times (n+1)$되는 행렬 $X^T \cdot X$의 역행렬을 계산합니다(n : 특성수). 이 역행렬의 계산 복잡도는 일반적으로 $O(n^{2.4})$에서 $O(n^3)$사이 입니다. 즉, 특성수가 두배로 늘어난다면 복잡도는 적게는 2^2.4배 크게는 2^3배만큼 늘어납니다. 특성수가 많아지면 정규방정식 처리 속도는 매우 느려 진다는 의미입니다.
그래도 이 공식(역행렬 계산함수)의 복잡도는 샘플 수에는 선형적이라고 합니다. 따라서 메모리 공간만 충분하다면 큰 훈련세트도 무리없이 처리할 수 있습니다.
정규 방정식이나 다른 알고리즘으로 학습시킨 선형 회귀 모델의 예측은 처리 속도가 매우 빠릅니다. 그리고 그 예측 계산 복잡도는 샘플 수와 특성 수에 비례합니다. 즉, 샘플 수나 특성 수가 두배로 늘어나면 처리에 걸리는 시간도 두배로 늘어난다는 것이죠.
특성수나 샘플수가 너무 커지면 처리 속도가 매우 느려 질 수 있습니다. 그럼 어떻게 해야 할까요?
특성이 매우 많고 훈련 샘플이 너무 많을 때 사용하기 적합한 알고리즘 중 하나가 바로 경사 하강법입니다. 경사 하강법은 어떤 비용함수에서 그 파라미터를 계속 조정해서 최적의 파라미터를 찾는 방법입니다. 파라미터의 그래디언트(Gradient)를 감소시키다가 그래디언트가 0이 되는 곳을 찾는 것입니다.
경사 하강법의 중요한 파라미터는 학습률(Learning late)입니다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 해야하고 학습률이 너무 크면 최솟값을 건너 뛰게 됩니다.
학습률이 너무 클 때
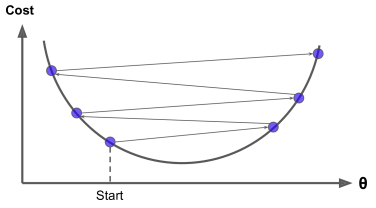
학습률이 너무 작을 때
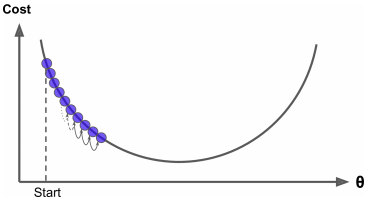
경사 하강법의 문제점
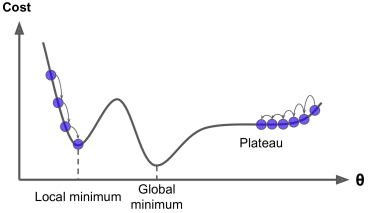
만약 비용 함수가 아니라 위와 같은 형태면 전역 최솟값(Global minimum)보다 덜 좋은 지역 최솟값(Local minimum)에 수렴할 수 있습니다.
(다행이 선형 회귀에 쓰이는 비용함수 MSE는 볼록 함수(Convex function)입니다. 전역 최솟값만 존재하죠.)
경사 하강법을 사용할 때는 특성들의 스케일이 같도록 만들어줘야 합니다. 그렇지 않으면 최솟값에 도달하는 시간이 오래 걸립니다. 따라서 스케일러(예를들면 사이킷런의 StandardSaler)를 사용해 스케일링을 해줍시다.
매 경사 하강법 스텝에서 전체 훈련세트 X에 대해 계산하는 방법입니다.
$\theta_j$에 대한 MSE의 편도함수
\(\frac{\partial}{\partial \theta_j} MSE(\theta) = \frac{2}{m} \sum_{i=1}^{m} (\theta^T \cdot x_i - y_i){x^i}_j\)
비용함수의 그래디언트 벡터
\(\nabla_\theta MSE(\theta) =
\begin{pmatrix}
\frac{\partial}{\partial \theta_0} MSE(\theta) \\
\frac{\partial}{\partial \theta_1} MSE(\theta) \\
\vdots \\
\frac{\partial}{\partial \theta_n} MSE(\theta) \\
\end{pmatrix} \\
= \frac{2}{m} X^T \cdot (X \cdot \theta - y)\)
배치 경사 하강법
\(\theta_{(next step)} = \theta - η \nabla_\theta MSE(\theta)\)
그래디언트가 양수면 다음 스텝의 $\theta$는 내려가야 하고 음수면 반대로 올라가야 하므로 η앞에 ‘-‘
가 붙었습니다. 만약 많은 수의 특성에서 선형회귀를 훈련시킨다면 정규 방정식보다 경사 하강법을 사용하는 편이 훨씬 빠릅니다.
eta = 0.1 # 학습률
n_iterations = 1000 ## 반복 횟수
m = 100
theta = np.random.randn(2,1) ## 정규분포 확률로 난수를 골라 2X1행렬에 넣음
for iteration in range(n_iterations):
gradients = 2/m * x_b.T.dot(x_b.dot(theta) - y) ## 그래디언트 벡터를 구함
theta = theta - eta * gradients ## 새로운 theta(파라미터)에 대입

그럼 최적의 학습률은 어떻게 찾을까요? 답은 그리드 탐색입니다. 그리드 탐색에서 수렴하는데 오래 걸리는 모델을 막기위해 반복횟수를 지정해야 합니다. 반복횟수를 크게 지정해 놓고 그래디언트 벡터 값이 어떤값(허용 오차)보다 작아지면 경사 하강법이 최솟값에 도달한 것이므로 알고리즘을 중지하는 방식으로 반복횟수를 지정합니다.
매 스텝마다 딱 한개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 그래디언트를 계산해서 파라미터를 훈련시키는 방법입니다. 작은 데이터만 처리하기 때문에 배치 경사 하강법 보다 훨씬 빠르고 메모리가 적게 들어 큰 훈련세트도 훈련시킬 수 있습니다. 확률적 경사 하강법은 지역 최솟값을 건너 뛸 수 있도록 도와주므로 배치 경사하강법 보다 전역 최솟값을 찾을 가능성이 높습니다. 확률적이기 때문에 최솟값에 근접하지만 최솟값에 안착하지는 못할 것입니다. 학습이 딜레마를 해결하는 방법은 학습률을 점진적으로 감소시키기는 것입니다.
확률적 경사 하강법 코드를 구현해 보겠습니다.
theta_path_sgd = []
m = len(x_b) # 100
np.random.seed(42)
n_epochs = 50 ## 한 반복에서 m번 되풀이 되는데, 이 때 한 번의 반복을 epoch라 한다.
t0, t1 = 5, 50 # 학습 스케줄 하이퍼파라미터(매 반복에서 학습률을 결정하는 파라미터)
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # 무작위 초기화
for epoch in range(n_epochs):
for i in range(m):
if epoch == 0 and i < 20 : #첫 반복의 20까지 #책에는 빠짐
y_predict = X_new_b.dot(theta)# 0과 2의 예측값 #책에는 빠짐
style = "b-" if i > 0 else "r--" # 0이 아닐 때는 파란 실선 0일 때는 빨간 점선 # 책에는 빠짐
plt.plot(X_new, y_predict, style)# 그래프를 그려라 # 책에는 빠짐
random_index = np.random.randint(m) ## 0부터 99사이의 값 중 하나를 랜덤으로 선택
xi = x_b[random_index:random_index+1] ## 데이터 중 하나의 샘플을 선택
yi = y[random_index:random_index+1] ## 선택한 샘플 데이터의 타겟값 선택
gradients = 2 * xi.T.dot(xi.dot(theta) - yi) ## 하나의 샘플로만 그래디언트 계산
eta = learning_schedule(epoch * m + i) ## epoc와 i가 감소 할 때마다 학습률 감소
theta = theta - eta * gradients ## 새로운 세타를 대입
theta_path_sgd.append(theta) ## 리스트에 튜닝돼서 나오는 theta다 넣음 # 책에는 빠짐
그래프를 그려보겠습니다.
plt.plot(X, y, "b.") # 책에는 빠짐
plt.xlabel("$x_1$", fontsize=18) # 책에는 빠짐
plt.ylabel("$y$", rotation=0, fontsize=18) # 책에는 빠짐
plt.axis([0, 2, 0, 15]) # 책에는 빠짐
# 책에는 빠짐
plt.show() # 책에는 빠짐
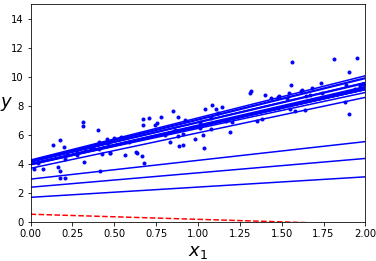
샘플들이 랜덤으로 선택이 되므로 한 에포크에서 어떤 샘플은 선택되지 않을 수 있습니다. 모든 샘플을 다 사용하게 하려면 한 에포크에서 훈련 세트를 섞고 하나씩 차례대로 하나씩 선택 후 다음 에포크에서 다시 훈련 세트를 섞어야 되는데 이렇게 하면 수렴 시간이 오래 걸립니다.
사이킷런에서 확률적 경사 하강법을 지원해 줍니다.
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=50, penalty=None, eta0=0.1, random_state=42)
## 최대 반복이 50번, panalty는 없음, eta0는 처음 학습률을 뜻함.
sgd_reg.fit(X, y.ravel()) ## y.ravel은 배열을 1차원 배열로 만들어주는 함수
미니 배치라 부르는 임의의 작은 샘플 세트에 대해 그래디언트를 계산하는 경사 하강법입니다. 확률적 경사 하강법보다 덜 불규칙하므로 최솟값에 더 가까이 도달하게 됩니다. 하지만 지역 최솟값에서 빠져나오기 힘들 수도 있습니다.
선형 회귀를 사용한 알고리즘 비교
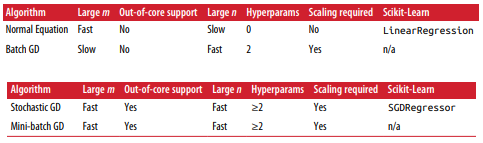
데이터의 개수가 많으면 배치 경사 하강법이 좋지 않습니다. 특성의 수(데이터의 벡터 차원)가 크다면 정규 방정식은 좋지 않습니다.
외부 메모리 학습 지원이란 컴퓨터 한 대의 메인 메모리에 들어갈 수 없는 아주 큰 데이터셋을 학습할 때 시스템에 온라인 학습 알고리즘을 사용하는 것입니다.
확률적 경사 하강법과 미니 배치 경사 하강법은 훈련할 때 샘플 하나 혹은 작은 묶음으로 훈련을 하므로 외부 메모리 학습이 가능합니다.
비선형 데이터를 학습하는데 특성의 거듭제곱을 새로운 특성으로 추가하고 추가한 데이터셋에 선형 모델을 훈련시키는 기법입니다.
간단한 샘플 데이터를 통해 구현해보겠습니다.
## 약간의 노이즈가 있는 2차 함수를 따르는 데이터셋 만들기
m = 100
X = 6 * np.random.rand(m, 1) - 3 ## -3부터 3 까지 랜덤하게
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1) ## y 값은 약간의 노이즈가 있는 2차 함수
## x,y를 그래프에 나타내면
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()
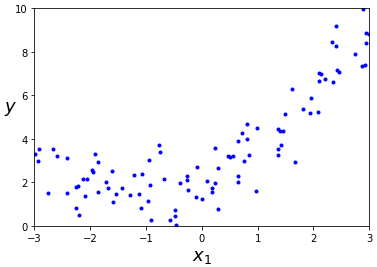
2차 함수의 그래프에 노이즈가 섞인 것이기 때문에 직선을 따르지 않습니다. 데이터의 제곱 값을 하나의 특성으로 추가하여 선형회귀를 하면 파라미터들을 훈련시킬 수 있습니다.
사이킷런의 PolynomieaFeatures로 데이터의 제곱값들을 특성에 추가합니다.
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
## degree=2 이면 제곱값들을 특성으로 추가 default는 2, include_bias는 x0=1을 추가할지 말지 경정, default 는 True
X_poly = poly_features.fit_transform(X)
X_poly[0] ## X데이터의 특성에 제곱값이 추가 됨.
array([2.1075118 , 4.44160599])
선형회귀로 훈련을 시켜보죠.
in_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
(array([2.09060416]), array([[1.00332088, 0.45237349]]))
$y$절편은 2.09060416, $x^2$의 계수는 1.00332088, $x$의 계수는 0.45237349로 예측을 하였습니다.
만약 특성의 개수가 하나가 아니라 두개라면 PolynomialFeatures가 주어진 차수까지 특성 간의 모든 교차항을 추가합니다. 예를 들어 특성 $a$와 $b$가 있고 차수가 $2$라면 $a^2$, $b^2$뿐만 아니라 $ab$도 추가됩니다.
얼마나 복잡한 모델을 사용할지 혹은 이 모델이 과대적합, 과소적합 되었는지 어떻게 알 수 있을까요? 바로 교차 검증을 사용하거나 학습 곡선을 살펴보는 것입니다. 학습 곡선은 훈련 세트와 검증 세트의 모델 성능을 훈련 세트 크기의 함수로 나타냅니다.
다음 코드는 학습 곡선을 그리는 함수를 정의한 것입니다.
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=20)
## X와 y 각각에서 20%를 test set(validate set)으로 쓰고 나머지는 train set으로 씀
## seed는 20
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m]) ## X의 train set의 1열에서 m열까지 모델에 훈련
y_train_predict = model.predict(X_train[:m]) ## 변수에 train set의 m열까지의 예측값을 넣음
y_val_predict = model.predict(X_val) ## 변수에 test set(validatae set)의 예측값을 넣음
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
# 리스트에 m열까지의 실제 값과 m열까지의 train set의 예측값의 에러를 넣음
val_errors.append(mean_squared_error(y_val, y_val_predict))
# 리스트에 validate set의 실제값과 예측값의 에러를 넣음
plt.plot(np.sqrt(train_errors), "r+-", linewidth=2, label='training')
## for문이 데이터 X의 크기에 따라서 돌아가므로 X축이 train set의 크기. y 값은 그에 따른 train set의 RMSE
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="test")
## X축은 똑같고 y 값은 test set(validate set)의 RMSE
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("size of train_set", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
선형 회귀의 학습곡선을 그려보겠습니다.
lin_reg= LinearRegression()
plot_learning_curves(lin_reg,X,y)
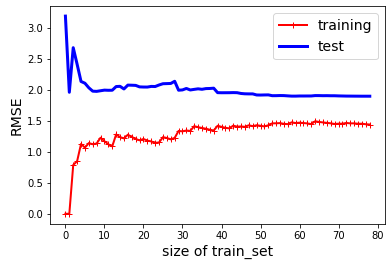
비선형이기 때문에 훈련데이터에 완벽히 훈련될 수 없으므로 훈련 데이터의 에러가 어느 정도에서 평평해집니다. 검증 데이터도 마찬가지로 훈련이 잘 되감에 따라 에러가 점점 감소하지만 훈련세트 아래로는 감소하지 않습니다. 이 학습 곡선은 과소적합의 예입니다. 수 곡선이 거의 평행을 이루는 구간이 있고, 꽤 높은 오차에서 서로 근접해 있습니다.
10차 다항 회귀 모델의 학습 곡선을 그려보겠습니다.
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("lin_reg", LinearRegression()),
]) ## 10차로 만들어주는PolynomialFeatures와 LinearREgression을 한번에 해주는 파이프라인
plot_learning_curves(polynomial_regression, X, y)
plt.axis([0, 80, 0, 3]) # 책에는 빠짐 # 책에는 빠짐
plt.show() # 책에는 빠짐
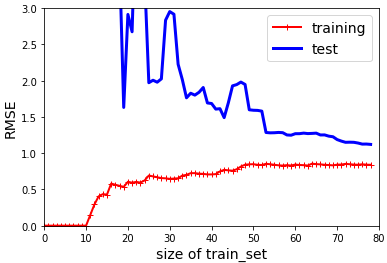
훈련 데이터의 오차가 선형 회귀 모델보다 낮습니다. 두 곡선 사이의 공간이 있는데 이것은 훈련 데이터에서의 성능이 더 좋다는 의미이고 훈련 데이터 셋에 과대적합 되어 있다는 말입니다. 과대적합이 되어 있을 때는 더 많은 훈련 데이터를 추가해서 검증 오차가 훈련 오차에 근접하도록 해야 합니다.