핸즈온 머신러닝
코딩관련깃허브
Author : Duck Hyeun, Ryu
안녕하세요. 팀 언플(Team Unsolved Problem)에 에디터 ㅋ헬 킴(Khel Kim), 김현호입니다. 오늘은 저희 팀에 오리, Duck Hyeun Ryu의 글을 정리 해서 업데이트하겠습니다.
오늘은 지난 시간 ‘Section 4.4 학습 곡선’에 이어서 ‘Section 4.5 규제가 선형 모델’에 들어가겠습니다.
[Hands-on ML] Chapter 4. Training Models(1)
그럼, 시작하겠습니다!
기본설정
import numpy as np
import os
import matplotlib
import matplotlib.pyplot as plt
import sklearn
np.random.seed(42)
matplotlib.rc('font', family='NanumBarunGothic')
plt.rcParams['axes.unicode_minus'] = False
과대적합을 줄이기 위해서는 모델의 자유도를 줄여야합니다. 이를 ‘모델을 제한한다’라고 표현합니다. 예를 들어 다항 회기 모델을 규제하는 방법은 다항식의 차수를 감소시키는 것입니다. 선형 회귀에서는 보통 모델의 가중치를 제한하여 규제를 가합니다. 가중치를 제한하는 3가지 규제 방법을 알아보도록 합시다.
첫 번째는 릿지 회귀(또는 티호노프 규제)입니다. 이는 규제가 추가된 선형 회귀 버전입니다. 규제항 $\alpha \sum^n_{i=1}\theta^2_i$가 비용 함수에 추가됩니다. 규제항은 훈련하는 동안에만 비용 함수에 추가됩니다. 모델의 성능은 규제가 없는 성능 지표로 평가합니다.
릿지 회귀의 비용 함수 수식
\[J(\theta) = MSE(\theta) + \alpha \frac{1}{2}\sum^n_{i=1}\theta^2_i\]하이퍼파라미터 $\alpha$는 모델을 얼마나 규제할지 조절합니다.
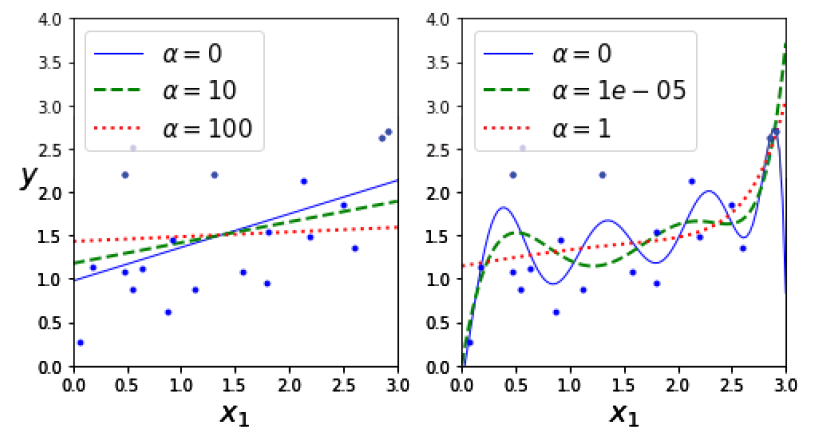
릿지 회귀는 입력특성의 스케일링에 민감하기 때문에 스케일을 맞추는 것이 중요합니다. 규제가 있는 모델은 대부분 마찬가지입니다.
릿지 회귀의 정규 방정식
\[\hat{\theta} = (X^T \cdot X +\alpha A)^{-1}\cdot X^T \cdot y\]다음은 사이킷런에서 정규방정식을 사용한 릿지 회귀를 적용하는 예입니다.
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
# solver의 기본값은 auto. 희소행렬이나 singular matrix가 아닐 경우 cholesky가 된다.
# 숄레스키를 사용하면 성능이 좋다?
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
## 결과
array([[1.55071465]])
다음은 확률적 경사 하강법을 사용했을 때 입니다.
sgd_reg = SGDRegressor(max_iter=5, penalty="l2", random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
## 결과
array([1.13500145])
penalty에 “l2”는 SGD가 비용 함수에 가중치 벡터의 $l_2$ norm의 제곱을 2로 나눈 규제항을 추가하게 됩니다. 즉, 릿지 회귀의 비용 함수에 추가된 항과 같습니다.
라쏘 회귀는 릿지 회귀와 비슷하지만 비용 함수의 규제를 $l_2$ norm 대신 $l_1$ norm을 사용합니다.
라쏘 회귀의 비용 함수
\[J(\theta) = MSE(\theta) + \alpha \sum^n_{i=1}|\theta_i|\]라쏘 회귀의 특징은 덜 중요한 특성의 가중치(파라미터)를 완전히 제거하려고 한다는 점입니다. 다시 말해, 라쏘 회귀는 0이 아닌 가중치가 적은 희소 모델을 만듭니다.
라쏘의 비용 함수는 $\theta_i$가 $0$일 때 미분이 가능하지 않습니다. 따라서 그래디언트 벡터 대신 서브그래디언트 벡터를 사용합니다.
서브그래디언트 벡터를 사용한 라쏘의 비용 함수
\(g(\theta, J) = \nabla_{\theta}MSE(\theta) + \alpha
\begin{pmatrix} sign(\theta_1) \\
sign(\theta_2) \\
\vdots \\
sign(\theta_n)
\end{pmatrix}\)
\(\mbox{ where } sign(\theta_i) =
\begin{cases}
-1 &\mbox{ if } \theta_i < 0 \\
0 &\mbox{ if } \theta_i = 0 \\
+1 &\mbox{ if } \theta_i > 0
\end{cases}\)
라쏘 회귀의 코드입니다.
## 라쏘 회귀를 코드로 해보자
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
##결과
array([1.53788174])
엘라스틱넷은 릿지 회귀와 라쏘 회귀를 절충한 모델입니다.
엘라스틱넷의 비용 함수
\[J(\theta) = MSE(\theta) + r\alpha \sum^n_{i=1}|\theta_i|+ \frac{1-r}{2}\alpha\sum^n_{i=1}\theta^2_i\]여기서 $r=1$ 이면 라쏘 회귀이고 $r=0$이면 릿지 회귀입니다.
## 엘라스틱넷을 사이킷런으로 구현해보자
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
## ㅣ1_ratio가 엘라스틱넷식의 r값
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
##결과
array([1.54333232])
그렇다면 어떤 것을 언제 써야할까요?
검증 에러가 최솟값에 도달하면 바로 훈련을 중지시키는 방법입니다.
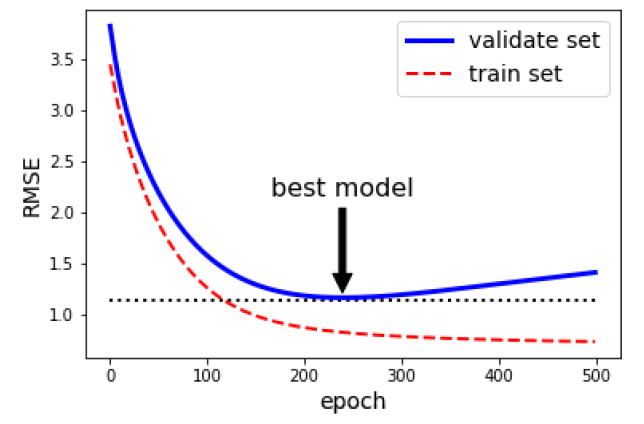이 그래프는 배치 경사하강법으로 훈련시킨 모델을 보여줍니다. 그래프를 보면 검증 에러가 점점 감소하다가 다시 증가합니다. 이 말은 모델이 훈련 데이터에 과대적합(overfitting)이 되기 시작했다는 말입니다. 따라서 검증에러가 최소값이 됐을 때 훈련을 멈춰야 합니다. 훈련을 멈추고 이 때의 파라미터를 쓰는 것을 조기 종료라고 합니다. 확률적 경사하강법이나 미니 배치 경사하강법은 곡선이 들쭉날쭉해서 최솟값을 찾기 어려울 수 있습니다. 검증 에러가 일정시간 동안 최솟값보다 내려가지 않을 때 최솟값일 때의 모델 파라미터를 사용해야합니다.
## 조기종료를 코드로 구현해보자
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler()),
]) ## 90제곱까지의 성분을 구하는 함수와 표준스케일링 파이프라인 구축
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
from sklearn.base import clone
sgd_reg = SGDRegressor(max_iter=1, warm_start=True, penalty=None,
learning_rate="constant", eta0=0.0005, random_state=42)
## warm_start = True면 fit 매서드가 호출될 때 이전 파라미터에서 훈련을 이어간다.
## learning_rate가 constant면 모든 eta는 eta0와 똑같음.
## penalty가 None이므로 규제는 없다.
minimum_val_error = float("inf") ## 플러스 무한대를 나타냄
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train)
y_val_predict = sgd_reg.predict(X_val_poly_scaled) # 다항회귀 예측값
val_error = mean_squared_error(y_val, y_val_predict) # MSE 에러값
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
## validate set의 에러값이 제일 작을 때의 에러값과 epoc 그리고 그 때의 훈련된 모델을 복사한다
어떤 회귀 알고리즘들은 분류에서도 사용할 수 있는데 로지스틱 회귀는 그 중 하나입니다. 어떤 샘플이 특정 클래스에 속할 확률을 추정하는데 널리 사용됩니다.
회귀 모델과 같이 가중치 합을 계산하지만 바로 결과를 출력하지 않고 결과값의 로지스틱을 출력합니다. 로지스틱은 0과 1사이의 값을 출력하는 시그모이드 함수입니다.
로지스틱은 기호로 $\sigma$로 표시합니다.
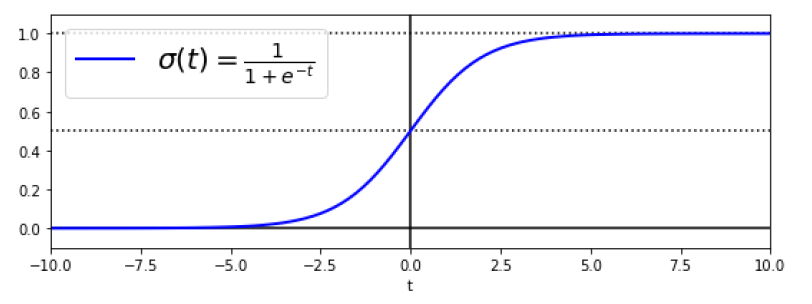$\hat{p}$은 확률이고 이에 대한 예측 $\hat{y}$은 이렇게 구합니다.
$t$가 양수일 때 $0.5$보다 크고 $t$가 음수일 때 $0.5$보다 작으므로 훈련된 모델이 양수일 때 $1$이라고 예측하고 훈련된 모델이 음수일 때 $0$이라고 예측합니다.
훈련의 목적은 양성 샘플($y=1$)에 대해서는 높은 확률을 추정하고 음성 샘플($y=0$)에 대해서는 낮은 확률을 추정하는 모델의 파라미터 벡터 $\theta$를 찾는 것입니다. 따라서 비 함수를 다음과 같이 정의합니다.
음성샘플(y=0)에 대해 확률을 0에 가깝게 추정하면 비용 함수가 줄어들고, 양성샘플(y=1)에 대해 확률을 1에 가깝게 추정하면 비용함수가 줄어듭니다.
로지스틱 회귀의 비용 함수(로그 손실이라고도 부릅니다)
한 번에 최적값을 찾아주는 방법은 없습니다. 그래도 전역 최솟값만 있는 볼록 함수이므로 경사 하강법을 써서 최적 파라미터를 찾을 수 있습니다.
로지스틱 회귀를 설명하기 위해 붓꽃 데이터셋을 사용하겠습니다. 이 데이터 셋은 3개의 품종에 속하는 붓꽃 150개의 꽃잎과 꽃받침의 너비와 길이를 담고 있습니다. 꽃잎의 너비를 기반으로 Iris-Versicolor 종을 감지하는 분류기를 만들어보겠습니다.
## 붓꽃의 종 중에 Iris-Versicolor종을 감지하는 분류기를 만들어보자
from sklearn import datasets
iris = datasets.load_iris() ## 붓꽃 데이터 셋이다.
list(iris.keys())
##결과
['data', 'target', 'target_names', 'DESCR', 'feature_names']
X = iris["data"][:, 3:] # 꽃잎 넓이
y = (iris["target"] == 2).astype(np.int) # Iris-Virginica가 2이므로 Virginica이면 1 아니면 0
로지스틱 회귀 모델을 훈련시켜보겠습니다.
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='liblinear', random_state=42)
log_reg.fit(X, y)
분류기에게 꽃잎의 너비가 0~3cm인 꽃에 대해 모델의 추정 확률을 계산해보겠습니다.
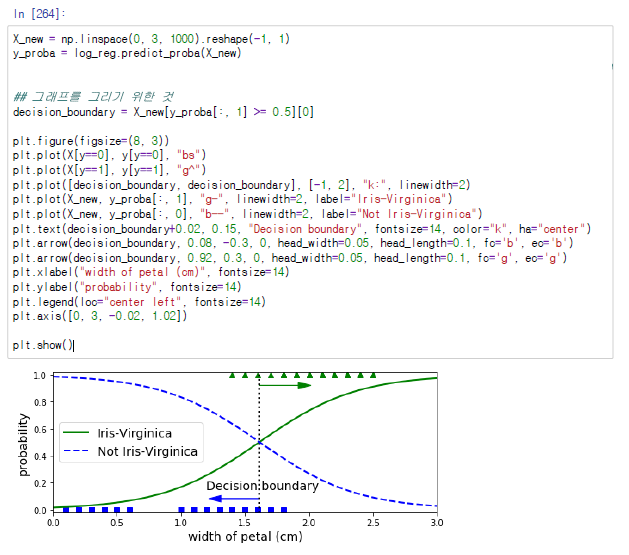
위에 그림에서 세모로 표시한 부분이 실제 타겟값이 Iris-Verginica인 샘플들이고, 밑에 네모는 나머지 두 품종입니다. 꽃잎의 길이가 2cm 이상인 샘플들은 무조건 Iris-Verginica이고 1cm 이하면 무조건 Iris-Verginica가 아닙니다. 하지만 그 사이는 확신할 수 없습니다. 따라서 모두의 확률이 50%인 1.6cm에서 우리의 결정 경계가(decision boundary)가 형성될 것입니다. 즉, 1.6cm보다 크면 Iris-Verginica라고 분류할 것이고 아니면 아니라고 분류할 것입니다.
log_reg.predict([[1.7], [1.5]])
##결과
array([1, 0])
로지스틱 회귀는 이진 분류만 할 수 있는 모델이 아니라 직접 다중 클래스를 분류할 수 있습니다. 이를 소프트맥스 회귀 또는 다항 로지스틱 회귀라고 합니다.
개념은 매우 간단한데, 샘플 $x$가 주어지면 먼저 소프트맥스 회귀 모델이 각 클래스 $k$에 대한 점수 $s_k(x)$를 계산하고, 그 점수에 소프트맥스 함수(또는 정규화된 지수 함수)를 적용하여 각 클래스의 확률을 추정합니다.
각 클래스는 자신만의 파라미터 벡터 $\theta^{(k)}$가 있습니다. 이 벡터들은 파라미터 행렬 $\Theta$에 행으로 저장됩니다.
샘플 $x$에 대해 각 클래스의 점수가 계산되면 소프트맥스 함수를 통과시켜 클래스 $k$에 속할 확률 $\hat{p}_k$를 추정할 수 있습니다.
로지스틱 회귀 분류기와 마찬가지로 소프트맥스 회귀 분류기는 추정 확률이 가장 높은 클래스를 선택합니다.
이 모델의 비용 함수는 크로스 엔트로피 비용 함수입니다. 이 비용 함수의 식은 아래와 같습니다.
$i$번째 샘플에 대한 타겟 클래스가 $k$일 때 $y^{(i)}_k$가 $1$이고, 그 외에는 $0$입니다.
이 비용 함수의 $\theta^{(k)}$에 대한 그래디언트 벡터
이제 각 클래스에 대한 그래디언트 벡터를 계산할 수 있으므로 비용 함수를 최소화하기 위한 파라미터 행렬 $\Theta$를 찾기 위해 경사 하강법을 사용할 수 있습니다.
꽃잎의 길이와 너비를 데이터로 주어진 샘플이 세 품종 중에 어느 품종에 속할지에 대한 분류를 할 수 있는 모델을 훈련시켜보겠습니다.
X = iris["data"][:, (2, 3)] # 꽃잎 길이, 꽃잎 넓이
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)
꽃잎의 길이가 5cm 길이가 2cm인 붓꽃을 발견했다고 할 때, 이 붓꽃이 어느 품족에 속해있을지 확률을 구해보겠습니다.
softmax_reg.predict([[5, 2]])
##결과
array([2])
3번째 클래스에 속해 있다고 말해주네요.
확률을 구해보겠습니다.
softmax_reg.predict_proba([[5, 2]])
##결과
array([[6.33134077e-07, 5.75276067e-02, 9.42471760e-01]])
저희는 4단원에서 선형 회귀 모델을 배우고 이를 규제하는 방법과 로지스틱 회귀를 배웠습니다. 다음 단원에서는 SVM 모델을 살펴보도록 하겠습니다.