핸즈온 머신러닝
코딩관련깃허브
안녕하세요. 팀 언플(Team Unsolved Problem)의 Polar B 입니다! 오늘 포스팅할 것은 핸즈온 머신러닝의 5장 Support Vector Machine 입니다. 머신러닝 모델 중에서도 꽤나 강력한 모델입니다.
강력한 만큼 내용도 쉽지 않습니다.저희는 먼저 SVM을 사이킷런으로 어떻게 사용할 수 있는지 배우고, 수학적으로는 어떻게 작동하는지 배우겠습니다. 한번 차근차근 책을 따라가 보도록 하겠습니다!
[Hands-on ML] Chapter 4. Training Models(2)
그럼 시작해볼까요?
기본설정
# 파이썬 2와 파이썬 3 지원
from __future__ import division, print_function, unicode_literals
# 공통
import numpy as np
import os
# 일관된 출력을 위해 유사난수 초기화
np.random.seed(42)
# 맷플롯립 설정
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# 한글출력
plt.rcParams['font.family'] = 'HCR Batang'
plt.rcParams['axes.unicode_minus'] = False
SVM은 머신러닝 모델중에 가장 강력하다고 할 수 있습니다. 인공신경망이 현대 기술에 힘입어 부상하기 전까지 가장 널리 사용되던 머신러닝 모델입니다. 이 모델은 선형, 비선형적인 데이터를 분류하거나 회기분석 할 수 있습니다. 또한 이상치 탐색에도 사용 가능합니다. 그 중에서도 특히 복잡한 분류를 잘 해내고 중간 크기의 데이터 셋에 적합합니다. 이번장에서는 SVM의 개념을 이해하고 작동원리를 알아보겠습니다.
SVM Classification을 클래스 사이에서 가장 폭이 넓은 도로를 찾는 것으로 생각 할 수 있습니다. 그래서 라지 마진 분류(large margin classification) 이라고도 불립니다.
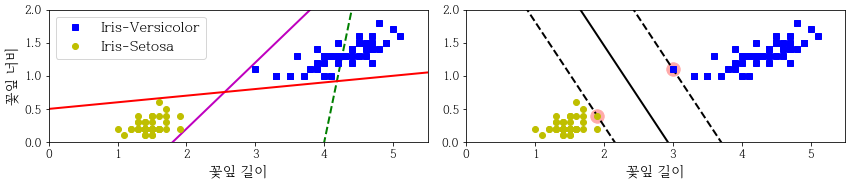
도로의 폭은 도로 경계에 위치한 샘플에 의해 전적으로 결정됩니다. 이 샘플을 서포트 벡터(Support Vector)라고 합니다.
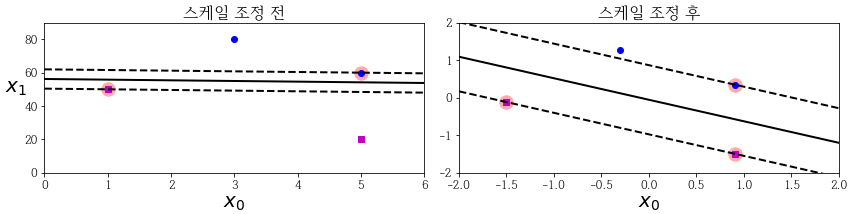
또한 특성의 스케일에 민감합니다. 따라서 StandardScaler를 사용하면 결정 경계가 훨씬 좋아집니다.
하드 마진 분류(Hard Margin Classification)은 모든 샘플이 도로 바깥쪽으로 올바르게 분류되어 있는 것입니다. 여기엔 두가지 문제점이 있습니다.
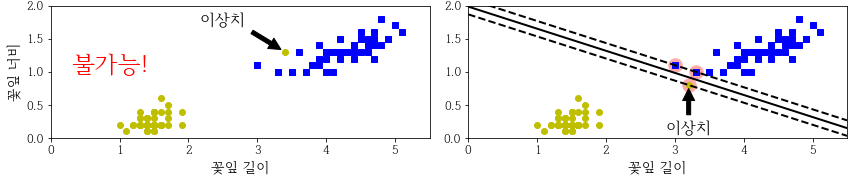
즉, 라지 마진 (도로의 폭을 가능한 한 넓게 유지하는 것) 과 마진 오류(margin violation : 샘플이 도로 중간이나 심지어 반대쪽에 있는 경우) 사이에 적절한 균형을 잡아야 합니다.
이것이 바로 소프트 마진 분류(Soft Margin Classification) 입니다.
사이킷런의 SVM모델에서는 C하이퍼파라미터를 사용해 이 균형을 조절할 수 있습니다.
C값을 줄이면 도로의 폭이 넓어지지만, 마진 오류도 커집니다.
iris 데이터 셋을 가지고 Iris-Virginia 품종을 감지하기 위한 선형 SVM모델을 훈련시켜보겠습니다.
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica, 아니면 0, 맞으면 1
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge", random_state=42)),
])
svm_clf.fit(X, y)
svm_clf.predict([[5.5, 1.7]]) # array([1.])
SVM분류기(LinearSVC)는 로지스틱 회기 분류기와는 다르게 클래스에 대한 확률을 제공하지 않습니다.
SVC모델은 probability = True로 매개변수를 지정하면 확률을 제공합니다.
SVC(kernel=”linear”, C=1)과 같이 SVC모델을 사용할 수 있습니다. 근데 큰 훈련세트에서 속도가 매우 느립니다
SGDClassifier(loss=”hinge”, alpha=1/(m * C)) (m은 샘플 수) 모델을 사용할 수도 있습니다. 큰 데이터 셋이나 온라인 학습으로 분류 문제를 다룰 때 유용합니다
LinearSVC는 규제에 편향을 포함시킵니다. 그래서 훈련 세트에서 평균을 빼서 중앙에 맞춰야 합니다. 이 일을 StandardScaler()가 해줄 수 있습니다. 그리고 loss 매개변수를 ‘hinge’로 지정해야 합니다.
여러가지 규제 설정을 비교하는 그래프를 만들어보겠습니다.
scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1, loss="hinge", random_state=42)
svm_clf2 = LinearSVC(C=100, loss="hinge", random_state=42)
scaled_svm_clf1 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf1),
])
scaled_svm_clf2 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf2),
])
scaled_svm_clf1.fit(X, y)
scaled_svm_clf2.fit(X, y)
# 스케일링이 되지 않은 파라미터로 변경
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
# 서포트 벡터 찾기 (libsvm과 달리 liblinear 라이브러리에서 제공하지 않기 때문에
# LinearSVC에는 서포트 벡터가 저장되어 있지 않습니다.)
t = y * 2 - 1
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
support_vectors_idx2 = (t * (X.dot(w2) + b2) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
svm_clf2.support_vectors_ = X[support_vectors_idx2]
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 6)
plt.xlabel("꽃잎 길이", fontsize=14)
plt.ylabel("꽃잎 너비", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
plt.subplot(122)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6)
plt.xlabel("꽃잎 길이", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
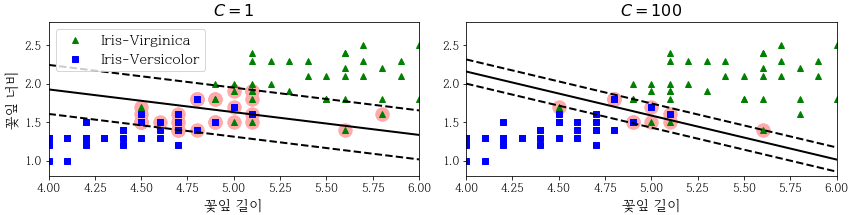
SVM 모델이 과대적합(Overfitting)이라면 C를 감소시켜 모델을 규제(Constraint)할 수 있습니다.
일반적으로 선형적으로 분류할 수 없는 데이터 셋이 더 많습니다.
비선형 데이터 셋을 다루는 한가지 방법은 (4장에서처럼) 다항 특성과 같은 특성을 더 추가하는 것입니다. 이렇게 하면 선형적으로 구분되는 데이터 셋을 만들 수 있습니다.
사이키런을 사용하여 구현할 때(4.3절 ‘다항 회귀’에서 소개한) PolynomialFeatures 변화기와 StandardScaler, LinearSVC를 연결하여 Pipeline을 만들면 좋습니다.
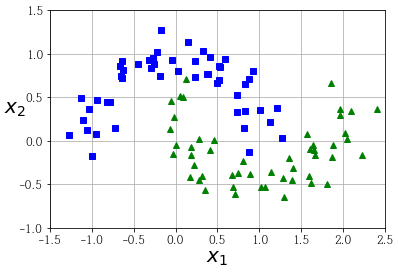
이것을 Moons 데이터 셋에 적용해 보겠습니다.
(Moons 데이터 셋은 그냥 반달 두개 모양의 데이터 셋입니다)
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", max_iter=2000, random_state=42))
])
polynomial_svm_clf.fit(X, y)
def plot_predictions(clf, axes):
x0s = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
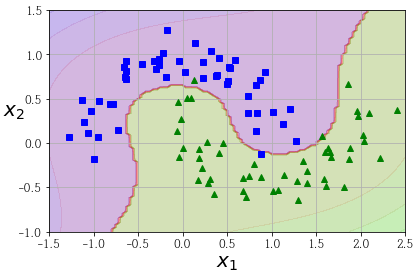
다항식 특성을 추가하는 것은 간단하지만, 한계가 있습니다. SVM을 가용할 때 Kernel trick이라는 수학적 기교를 적용할 수 있습니다. 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있는 트릭입니다. 이는 SVC 파이썬 클래스에 구현되어 있습니다.
moons 데이터셋으로 테스트해보겠습니다
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
poly_kernel_svm_clf.fit(X, y)
poly100_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
poly100_kernel_svm_clf.fit(X, y)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)
plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
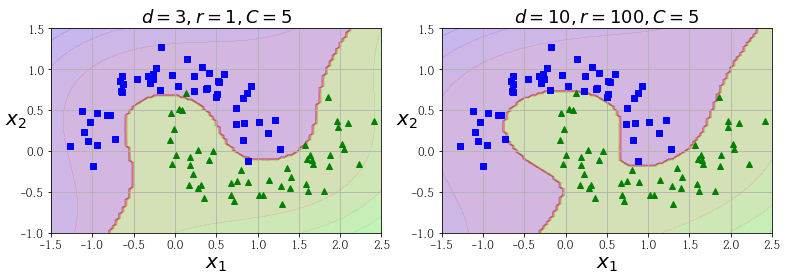
매개 변수
모델이 과대적합이라면 다항식의 차수를 줄여야 합니다(반대면 반대로).
적절한 하이퍼파라미터 찾는 일반적인 방법은 (2장에서의)그리드 탐색이 있습니다.
비선형 특성을 다루는 또 다른 기법입니다.
각 샘플이 특정 랜드마크(landmark) 와 얼마나 닮았는지 측정하는 유사도 함수(similarity function) 로 계산한 특성을 추가합니다.
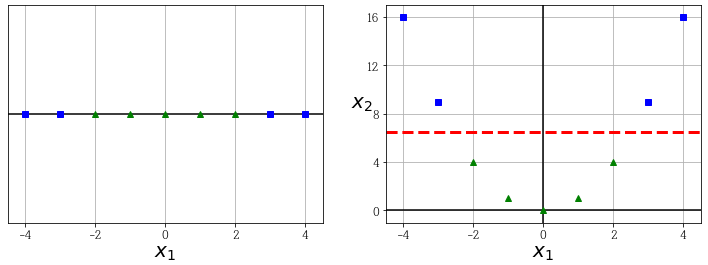
앞서 본 1차원 데이터셋에 두개의 랜드마크 x = -2와 x = 1을 추가합니다. 그리고 gamma = 0.3인 가우시안 방사 기저 함수(Radial Basis Function, RBF) 을 유사도 함수로 정의합니다.
Gaussian RBF
\(\phi_γ (x,\ell) = exp(-γ \Vert x-\ell \Vert^2)\)
이 함수의 값은 0부터 1까지 변화하며 종모양으로 나타납니다. gamma는 0보다 커야 됩니다. 값이 작을수록 폭이 넓은 종 모양이 됩니다.
이를 코드로 구현해보겠습니다.
def gaussian_rbf(x, landmark, gamma):
return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)
gamma = 0.3
x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)
XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk==1], np.zeros(5), "g^")
plt.plot(x1s, x2s, "g--")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"유사도", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
xy=(X1D[3, 0], 0),
xytext=(-0.5, 0.20),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.text(-2, 0.9, "$x_2$", ha="center", fontsize=20)
plt.text(1, 0.9, "$x_3$", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk==0], XK[:, 1][yk==0], "bs")
plt.plot(XK[:, 0][yk==1], XK[:, 1][yk==1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$ ", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left(\mathbf{x}\right)$',
xy=(XK[3, 0], XK[3, 1]),
xytext=(0.65, 0.50),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])
plt.subplots_adjust(right=1)
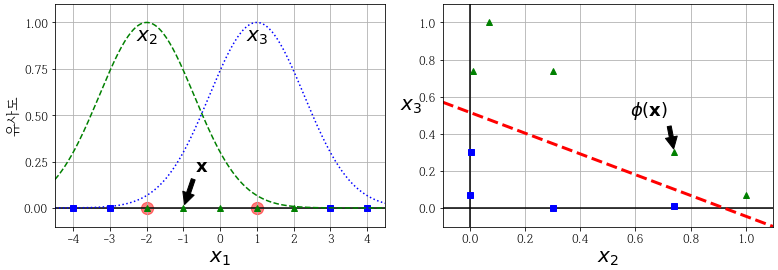
x = -1 을 살펴보겠습니다. 첫번째 랜드마크(-2)에서 1떨어져 있고, 두번째 랜드마크(1)에서 2 떨어져 있습니다. 그래서 새로 만든 특성은 (가우시안RBF 의 x에 각각 넣어주면) (0.74,0.30)이 됩니다. 이런 식으로 해서 변환해주면 선형적으로 구분을 할 수 있게 됩니다.
x1_example = X1D[3, 0]
for landmark in (-2, 1):
k = gaussian_rbf(np.array([[x1_example]]), np.array([[landmark]]), gamma)
print("Phi({}, {}) = {}".format(x1_example, landmark, k))
Phi(-1.0, -2) = [0.74081822]
Phi(-1.0, 1) = [0.30119421]
그럼 랜드마크를 어떻게 선택할까요? 바로 모든 샘플에 랜드마크를 설정해보는 것 입니다. (생각만 해도 비효율적일 것 같지만…) 차원이 매우 커지고 따라서 변환된 훈련 세트는 선형적으로 구분될 ‘가능성’이 높아집니다.
유사도 특성도 머신러닝 알고리즘에 유용하게 사용될 수 있습니다. 근데 앞에 설명했던 문제가 있습니다. (시간이 오래 걸리는 것. 특히, 데이터가 크면 정말 오래 걸림)
이것을 SVM에선 그냥 가우시안 RBF 커널을 추가 하는 것으로 같은 효과를 얻을 수 있습니다.
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)
from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(11, 7))
for i, svm_clf in enumerate(svm_clfs):
plt.subplot(221 + i)
plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
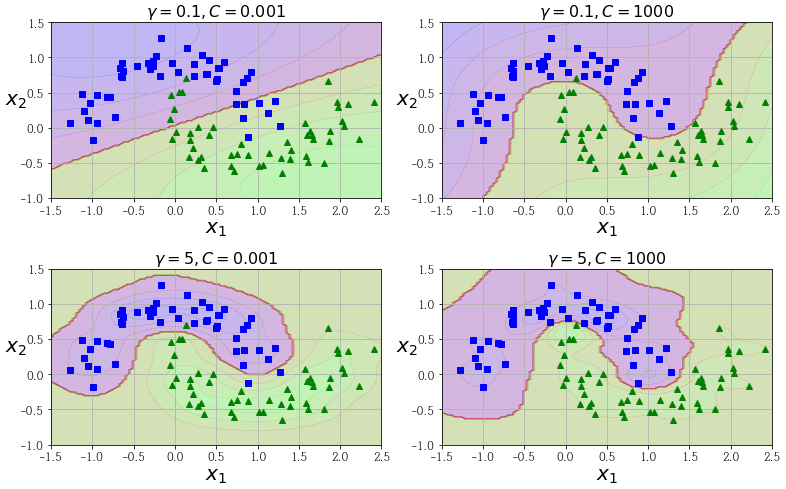
gamma가 높아지면 종 모양 그래프가 좁아져서 각 샘플의 영향 범위가 줄어듭니다. 즉, 경계가 데이터들을 따라 구불구불해집니다.
반대로 낮으면 샘플이 넓은 범위에 걸쳐 영향을 주므로 결정경계가 부드러워집니다.
따라서, 모델이 과대적합일 경우엔 감소시켜야 되고 과소적합일 경우에는 증가시켜야 됩니다.
문자열 커널(string kernel) (e.g. string subsequence kernel, levenshtein distance 기반의 커널) 등의 특정 데이터에 특화된 커널도 있습니다.
그럼 우린 이 여러 커널 중에 어떤 것을 사용해야 할까요?
책에서는 경험적으로 언제나 선형커널부터 시도해보라고 합니다. 특히, 훈련세트가 아주 크거나 특성 수가 많을 경우에 그러합니다. 훈련 세트가 너무 크지 않다면 가우시안 RBF 커널을 시도해보면 좋다고 합니다. 컴퓨터가 좋으면 교차검증과 그리드 탐색으로 여러 커널을 시도해보는 것도 나쁘지 않다고 합니다.
앞장에서 다루었듯이 O표기법으로 복잡도를 나타냅니다.

SVM은 회귀에도 쓸 수 있습니다. 어떻게 하는 걸까요? 바로 제한된 마진 오류(즉, 도로 밖 샘플)안에서 도로 안에 가능한 한 많은 샘플이 들어가게 학습하면 됩니다. 도로의 폭은 하이퍼파라미터로 조절합니다.
코드를 통해 알아보겠습니다.
# 무작위로 데이터 생성
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel()
#LinearSVR을 사용해 선형 SVM 회귀를 적용
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)
svm_reg1 = LinearSVR(epsilon=1.5, random_state=42)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)
def find_support_vectors(svm_reg, X, y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
return np.argwhere(off_margin)
svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)
eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X, y, "bo")
plt.xlabel(r"$x_1$", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plt.axis(axes)
plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
#plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg1.epsilon], "k-", linewidth=2)
plt.annotate(
'', xy=(eps_x1, eps_y_pred), xycoords='data',
xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
)
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.subplot(122)
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
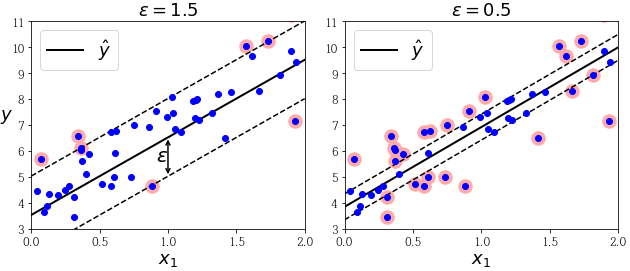
왼쪽은 마진을 크게하고 오른쪽은 마진을 작게 해보았습니다 근데 모델 예측에 큰 차이가 없군요. 이런 것을 epsilon-insensitive 라고 말합니다.
선형 모델을 구현했다면 이번에는 비선형 모델을 구현해보겠습니다.
np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()
from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", gamma='auto', degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X, y)
from sklearn.svm import SVR
svm_poly_reg1 = SVR(kernel="poly", gamma='auto', degree=2, C=100, epsilon=0.1)
svm_poly_reg2 = SVR(kernel="poly", gamma='auto', degree=2, C=0.01, epsilon=0.1)
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)
plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.subplot(122)
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
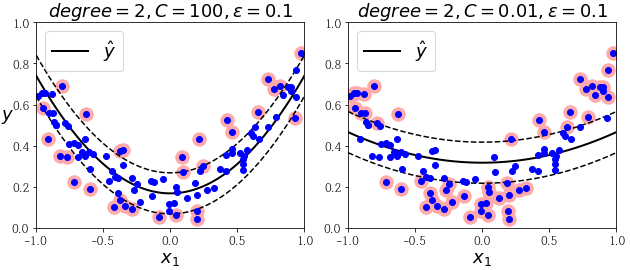
(왼쪽은 규제가 거의 없고(큰 C), 오른쪽은 규제가 많음(작은 C))
예상했겠지만 LinearSVR은 LinearSVC의 회기 버전이고 SVR 은 SVC의 회기 버전입니다.
훈련에 필요한 시간 또한 Classification 때와 비슷합니다.
편향을 $b$, 특성의 가중치 벡터를 $w$라고 합니다.
$w^T \cdot x + b = w_1x_1 + \cdots + w_n x_n + b$를 계산해서 새로운 샘플 $x$의 클래스를 예측합니다.
\(\hat{y} =
\begin{cases}
0 & w^T \cdot x + b \lt 0 \text{일 때} \\
1 & w^T \cdot x + b \geq 0 \text{일 때}
\end{cases}\)
iris 데이터를 다시 가지고와 보겠습니다.
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica
from mpl_toolkits.mplot3d import Axes3D
def plot_3D_decision_function(ax, w, b, x1_lim=[4, 6], x2_lim=[0.8, 2.8]):
x1_in_bounds = (X[:, 0] > x1_lim[0]) & (X[:, 0] < x1_lim[1])
X_crop = X[x1_in_bounds]
y_crop = y[x1_in_bounds]
x1s = np.linspace(x1_lim[0], x1_lim[1], 20)
x2s = np.linspace(x2_lim[0], x2_lim[1], 20)
x1, x2 = np.meshgrid(x1s, x2s)
xs = np.c_[x1.ravel(), x2.ravel()]
df = (xs.dot(w) + b).reshape(x1.shape)
m = 1 / np.linalg.norm(w)
boundary_x2s = -x1s*(w[0]/w[1])-b/w[1]
margin_x2s_1 = -x1s*(w[0]/w[1])-(b-1)/w[1]
margin_x2s_2 = -x1s*(w[0]/w[1])-(b+1)/w[1]
ax.plot_surface(x1s, x2, np.zeros_like(x1),
color="b", alpha=0.2, cstride=100, rstride=100)
ax.plot(x1s, boundary_x2s, 0, "k-", linewidth=2, label=r"$h=0$")
ax.plot(x1s, margin_x2s_1, 0, "k--", linewidth=2, label=r"$h=\pm 1$")
ax.plot(x1s, margin_x2s_2, 0, "k--", linewidth=2)
ax.plot(X_crop[:, 0][y_crop==1], X_crop[:, 1][y_crop==1], 0, "g^")
ax.plot_wireframe(x1, x2, df, alpha=0.3, color="k")
ax.plot(X_crop[:, 0][y_crop==0], X_crop[:, 1][y_crop==0], 0, "bs")
ax.axis(x1_lim + x2_lim)
ax.text(4.5, 2.5, 3.8, "결정 함수 $h$", fontsize=15)
ax.set_xlabel(r"꽃잎 길이", fontsize=15, labelpad=15)
ax.set_ylabel(r"꽃잎 너비", fontsize=15, rotation=25, labelpad=15)
ax.set_zlabel(r"$h = \mathbf{w}^T \mathbf{x} + b$", fontsize=18, labelpad=10)
ax.legend(loc="upper left", fontsize=16)
fig = plt.figure(figsize=(11, 6))
ax1 = fig.add_subplot(111, projection='3d')
plot_3D_decision_function(ax1, w=svm_clf2.coef_[0], b=svm_clf2.intercept_[0])
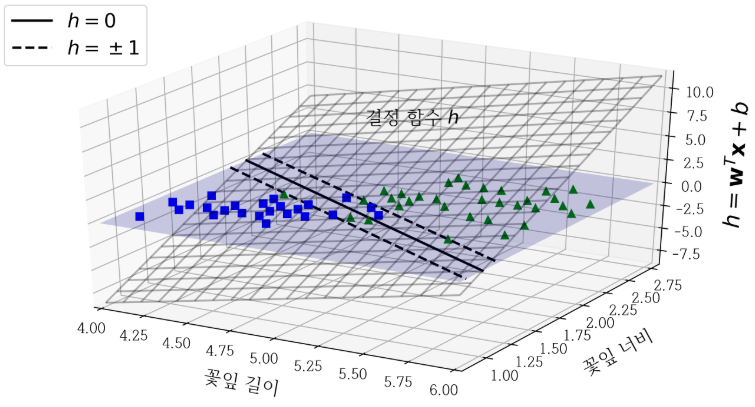
결정 경계는 결정 함수 h가 0인 점들로 이루어져 있습니다. 이는 두 평면의 교차점입니다. 점선은 결정 함수의 값이 1 또는 -1인 점들을 나타냅니다. 선형 SVM분류기를 훈련한다는 것은 가능한한 마진을 크게 하는 $w$와 $b$를 찾는 것입니다.
작은 가중치 벡터가 라지 마진을 만든다고 합니다.
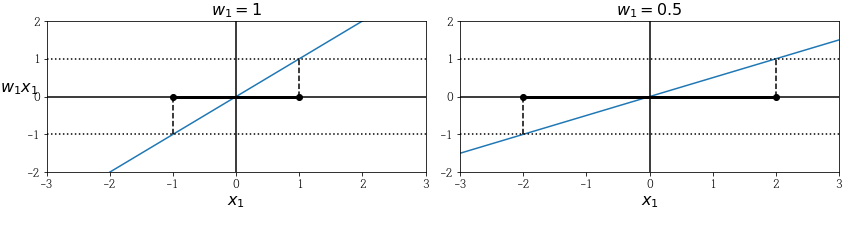
(그림에서 알 수 있듯이 $w_1$이 작아지자 x의 범위가 (-1,1)에서 (-2,2)로 늘어났습니다.)
우리의 목적은 마진을 크게 해서 경계를 확실하게 만드는 것입니다. 따라서 $||w||$를 최소화해야 합니다.
마진 오류를 하나도 만들지 않는 하드마진을 구현하려면,
\({\operatorname{minimize} \atop w,b} \frac{1}{2} w^T \cdot w\)
\(\text{[조건]} i=1,2, \cdots, m \text{일 때} \quad t^{(i)}(w^T \cdot x^{(i)} + b) \geq 1\)
오류를 어느정도 허용하면서 과대적합하지 않는 소프트 마진을 구현하려면,
\({\operatorname{minimize} \atop w,b,\zeta} \frac{1}{2} w^T \cdot w + C \sum_{i=1}^{m} \zeta^{(i)}\)
\(\text{[조건]} i=1,2, \cdots, m \text{일 때} \quad t^{(i)}(w^T \cdot x^{(i)} + b) \geq 1-\zeta^{(i)} 그리고 \zeta^{(i)} \geq 0\)
소프트 마진 분류기에선 슬랙 변수(slack ariable) 을 도입합니다. 이것은 i번째 샘플이 얼마나 마진을 위반할지 결정합니다.
슬랙 변수를 작게 하면 마진 오류도 작아지지만 과대적합이 일어날 수 있습니다. C는 전체 슬랙 변수를 조절해주는 하이퍼파라미터입니다.
선형적인 제약조건이 있는 볼록 함수의 이차 최적화 문제를 콰드라틱 프로그래밍(Quadratic Programming, QP) 문제라고 합니다. 여러 테크닉으로 QP를 푸는 알고리즘이 많이 있지만 이 책에서는 다루고 있지 않습니다.
일반적 문제공식은
\({\operatorname{minimize} \atop p} \frac{1}{2} p^T \cdot H \cdot p + f^T \cdot p\)
\(\text{[조건]} A \cdot p \leq b\)
\(\text{여기서}
\begin{cases}
p\text{는 } n_p\text{차원의 벡터}(n_p = \text{모델 파라미터 수}) \\
H\text{는 } n_p \times n_p \text{크기 행렬} \\
f\text{는 } n_p\text{차원의 벡터} \\
A\text{는 } n_c \times n_p \text{크기 행렬(}n_c\text{)제약 수} \\
b\text{는 } n_c \text{차원의 벡터} \\
\end{cases}\)
다음과 같이 QP 파라미터를 지정하면 하드 마진을 갖는 선형 SVM분류기의 목적함수를 간단하게 검증할 수 있습니다.
하드 마진 선형SVM 분류기를 훈련시키는 한 방법은 준비된 QP알고리즘에 관련 파라미터를 전달하기만 하면 됩니다. 하지만 커널 트릭을 사용하려면 제약이 있는 최적화 문제를 다른 형태로 바꿔야 합니다.
원 문제(Primal problem) 라는 제약이 있는 최적화 문제가 주어지면 쌍대 문제(Dual problem) 라는 다른 문제로 표현 가능합니다. 그리고 그것은 라그랑지 승수법(Lagrange multiplier method) 를 이용해서 풉니다.

훈련 샘플 수가 특성 개수보다 작을 때 원 문제보다 쌍대 문제를 푸는 것이 더 빠릅니다. 그리고 중요한 건 쌍대 문제에선 커널 트릭을 쑬 수 있습니다.
데이터 셋의 차원을 한 차원 높여 주는 것을 커널 트릭이라고 합니다. 예를 들면 moons 데이터셋과 같은 2차원 데이터셋을 2차 다항식 커널을 통해 3차로 만들어줄 수 있습니다. 그럼 2차원에서 선형적으로 구분하지 못하던 것도 한단계 높은 차원으로 바꿈으로써 선형적으로 구분할 수 있습니다.

보면 변환된 벡터의 점곱이 원래 벡터의 점곱의 제곱과 같다는 걸 알 수 있습니다. 즉 차원을 높인다고 해도 계산이 어렵지 않다는 것입니다.
다음은 자주 사용되는 커널의 일부입니다.

머서의 정리
특정 수학적 조건을 만족할 때 위와 같은 높은 차원으로 mapping 해주는 함수가 존재한다는 것을 증명하는 정리입니다.

온라인 학습은 새로운 샘플이 생겼을 때 점진적으로 학습하는 것입니다.
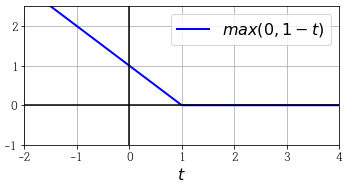
힌지 손실
max(0,1-t)함수를 hinge loss function 이라고 부릅니다.
저희는 5단원에서 SVM모델의 사용방법과 이론을 배웠습니다. 다음 단원에서는 결정 트리를 살펴보도록 하겠습니다.