[Hands-On ML] Chapter 6. Decision Tree

핸즈온 머신러닝
코딩관련깃허브

Author : Duck Hyeun, Ryu

안녕하세요. 팀 언플(Team Unsolved Problem)에 에디터 ㅋ헬 킴(Khel Kim), 김현호입니다.
오늘은 지난 시간 ‘Ch 5. SVM’에 이어서 ‘Ch 6. Decision Tree’에 들어가겠습니다.
[Hands-on ML] Chapter 5. Support Vector Machine

그럼, 시작하겠습니다!

기본설정

# 공통
import numpy as np
import os

# 일관된 출력을 위해 유사난수 초기화
np.random.seed(42)

# 맷플롯립 설정
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

# 한글출력
matplotlib.rc('font', family='NanumBarunGothic')
matplotlib.rcParams['axes.unicode_minus'] = False

# 작업할 디렉토리
PROJECT_ROOT_DIR = "C:\\Python\\MLPATH" ##파이썬 디렉토리 저장
CHAPTER_ID = "decision_trees"
IMAGE_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)

def image_path(fig_id, image_path_k2h=IMAGE_PATH):
    return os.path.join(image_path_k2h, fig_id) ##사진을 저장할 위치

6.0. Introduction
6.1. Training and Visualizing a Decision Tree
6.2. Making Predictions
6.3. Estimating Class
6.4. The CART Training Algorithm
6.5. Computational Complexity
6.6. Gini Impurity or Entropy
6.7. Regularization Hyperparameters
6.8. Regression
6.9. Instability

6.0 Introduction

결정트리는 분류와 회귀 작업 그리고 다중출력 작업도 가능한 머신러닝 모델입니다. 복잡한 데이터셋도 학습할 수 있고, 랜덤 포레스트의 기본 구성 요소입니다.

6장에서는 훈련, 시각화, 예측 방법, CART 훈련 알고리즘, 규제, 회귀 문제에 적용, 제약사항등을 살펴보겠습니다.

6.1 Training and Visualizing a Decision Tree

4장에서 사용한 붓꽃 데이터셋으로 DecisionTreeClassifier를 훈련 시켜보겠습니다.

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris() ##모듈 안 load_iris는 function으로 정의되어있고, 함수를 불러야 데이터 Bunch를 얻을 수 있음.

X = iris.data[:, 2:] ## data attiribute: [sepal length, sepal width, petal legth, petal width] ## 꽃받침, 꽆잎
y = iris.target

Bunch

잠시 Bunch 자료형에 대해서 알아보겠습니다.

print(type(iris))

## 결과
<class 'sklearn.utils.Bunch'>

Bunch 자료형은 사이킷런에 내장되어있는 자료형으로서 파이썬의 기본 자료형인 딕셔너리와 거의 비슷하게 사용됩니다. 차이가 있다면, 파이썬 자료형인 딕셔너리에서는 value값을 dic[‘key_name’]으로 구해야 했다면, Bunch 자료형은 bunch[‘key_name’]과 bunch.key_name으로 구할 수 있습니다.

print('\n', iris.data.shape) ##데이터 개수와 특징 개수 확인
print('\n \n', iris.DESCR) ##Bunch안에 이 데이터가 어떤 데이터인지 알려주는 key와 value가 있음

다시 돌아와서…

우리의 결정트리를 훈련시켜보겠습니다.

tree_clf = DecisionTreeClassifier(max_depth=2)
##사용하려는 모델을 정의하고
tree_clf.fit(X, y)
##우리가 가진데이터를 집어 넣음

끝입니다!! ㅋㅋㅋㅋㅋㅋ 쉽죠? 결정트리의 강점 중 하나는 훈련된 결정트리를 시각화 할 수 있습니다. 보통 머신러닝 모델의 내부는 블랙박스 취급을 합니다. 즉, 우리 모델이 어째서 결과를 이렇게 저렇게 도출했는지 알 수 없다는 것입니다. 하지만 결정트리는 화이트박스라 하여 어째서 결정트리가 이렇게 저렇게 판단했는지 알 수 있다는 것입니다.

##개인적으로 홈 디렉터리를 바꿔서 책에 있는 코드가 적용되지 않음
##따로 만듦
from sklearn.tree import export_graphviz
def export_graphviz_k2h(ML_algorithms, image_path_k2h=IMAGE_PATH):
    if not os.path.isdir(image_path_k2h):#github 코드로는 작동이 안되서
        os.makedirs(image_path_k2h) ##직접 image 폴더, decision_trees 폴더를 만듦
    export_graphviz(
    ML_algorithms,
    out_file=image_path("iris_tree.dot"), ##C:\Python\image\decisiontrees\iris_tree.dot
    feature_names=iris.feature_names[2:],
    class_names=iris.target_names,
    rounded=True, ##박스 생김새
    filled=True ##박스 생김새
        )

export_graphviz_k2h(tree_clf) ##dot 파일을 만들어줌

여기서 graphviz 프로그램을 따로 다운로드 하셔야합니다. 책에서는 명령 프롬프트에서

dot -Tpng iris_tree.dot -o iris_tree.png

를 실행해서 png 파일을 만들지만, 위에 박해선 번역가님 깃허브에 있는 쥬피터 노트북에서 png파일을 바로 볼 수 있는 코드가 있습니다.

import graphviz
with open("images/decision_trees/iris_tree.dot") as f:
    dot_graph = f.read()

dot = graphviz.Source(dot_graph)
dot.format = 'png'
dot.render(filename='iris_tree', directory='images/decision_trees', cleanup=True)
dot ##시스템 변수, PATH에 graphviz가 있어야함

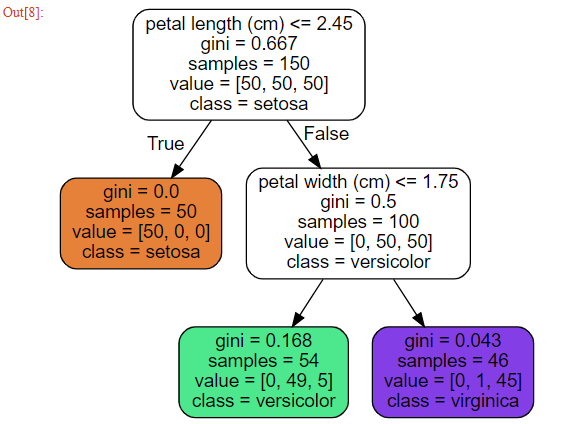
tree1

6.2 Making Predictions

일단 결정트리에게 예측을 맡기기 전에 용어를 먼저 정리하겠습니다.

root node: 깊이가 0인 맨 꼭대기의 노드
child node: 한 노드에서 나오는 다른 노드
leaf node: child node를 가지지 않는 노드

결정트리가 예측하는 방식은 다음과 같습니다.

petal length가 2.45cm보다 긴 새로운 꽃을 발견했다고 하면
root node의 오른쪽 child node로 이동합니다.
오른쪽 child node는 leaf node가 아니여서, 추가로 petal width를 검사합니다.
왼쪽 혹은 오른쪽 leaf node로 이동합니다.

Note. 결정트리의 여러 장점 중 하나는 데이터 전처리가 거의 필요하지 않다는 것입니다. 특히 특성의 스케일을 맞추거나 평균을 원점에 맞추는 작업이 필요하지 않습니다.

tree1 이번엔 박스 내부 용어를 살펴보겠습니다.

sample - 적용된 훈련 샘플의 개수
value - 그 노드에서 각 class에 있는 훈련 샘플의 개수
gini - 불순도 (gini는 불순도 측정 방식 중 하나, 엔트로피를 쓸 때도 있음, 엔트로피 방정식은 뒤에서 설명)

지니계수
$G_i = \sum^n_{k=1} p_{i,k} (1 - p_{i,k}) = 1 - \sum^n_{k=1} p^2_{i,k}$
where $p_{i,k}$ is the ratio of class $k$ instances among the training instance in the $i^{th}$ node.

질문.

지니 계수는 불순도를 잘 나타내주는 지표인가?

이 질문을 해결하려면 불순도 측정 방식을 잘 정의하고(수학의 metric처럼), 그 특성을 가지고 지니 계수가 불순도를 측정하는 방식에 부합하는지를 살펴봐야 할 듯. 따라서 ‘불순한 정도를 측정한다’라는 말을 수학적으로 정의해줘야할 것같다.

Note. sklearn은 이진 트리 만 만드는 CART알고리즘을 사용합니다(CART알고리즘은 뒤에서 추가로 설명). 따라서, leaf node를 제외한 모든 node는 child node를 두 개씩 가지게 됩니다.

from matplotlib.colors import ListedColormap

def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
    x1s = np.linspace(axes[0], axes[1], 100)
    x2s = np.linspace(axes[2], axes[3], 100)
    x1, x2 = np.meshgrid(x1s, x2s)
    X_new = np.c_[x1.ravel(), x2.ravel()]
    y_pred = clf.predict(X_new).reshape(x1.shape)
    custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
    plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
    if not iris:
        custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
        plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
    if plot_training:
        plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
        plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
        plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^")
        plt.axis(axes)
    if iris:
        plt.xlabel("꽃잎 길이", fontsize=14)
        plt.ylabel("꽃잎 너비", fontsize=14)
    else:
        plt.xlabel(r"$x_1$", fontsize=18)
        plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
    if legend:
        plt.legend(loc="lower right", fontsize=14)

plt.figure(figsize=(8, 4))
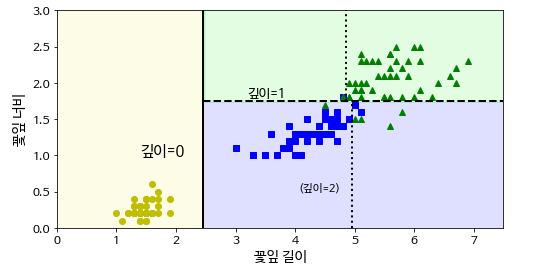
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "깊이=0", fontsize=15)
plt.text(3.2, 1.80, "깊이=1", fontsize=13)
plt.text(4.05, 0.5, "(깊이=2)", fontsize=11)

plt.show()

tree2

max_depth를 0,1,2로 설정함에 따라 결정 경계가 추가로 생깁니다.

6.3 Estimation Class

결정트리는 한 샘플이 특정 클래스 k에 속할 확률을 추정할 수도 있습니다.
샘플을 알고리즘에 적용하면 leaf node를 찾고, 그 노드에 있는 클래스 k의 훈련 샘플 비율을 반환합니다.
클래스를 하나 예측한다면 (tree_clf.predict으로 예측 값을 출력한다면), 가장 높은 확률을 가진 클래스를 출력합니다.

tree_clf.predict_proba([[5, 1.5]])

## 결과
array([[0.        , 0.90740741, 0.09259259]])

tree_clf.predict([[5, 1.5]])

## 결과
array([1])

6.4 The CART Training Algorithm

CART란 Classification And Regression Tree Algorithm의 약자입니다. 먼저 훈련 세트를 하나의 특성 $k$와 임곗값 $t_k$를 사용해 두 개의 서브셋으로 나눕니다.

$k$와 $t_k$를 고르는 방식
가장 순수한(불순도가 낮은) 서브셋으로 나눌 수 있는 ($k$,$t_k$) 짝을 찾음
$J_{k, t_k} = \frac{m_{left}}{m} G_{left} + \frac{m_{right}}{m} G_{right}$
where $G_{left/right}$ measures the impurity of the left/right subset, and $m_{left/right}$ is the number of instances in the left/right subset.
Note. Gain함수: 특성과 임계값에 따라 얻을 수 있는 정보량
$Gain(k) = Entropy(X) - J_{k,t_k}$
gain함수가 높은 특성 k를 선택해야함

이 과정에서 질문이 몇 개 생겼는데 혹시 답을 아신다면 댓글 혹은 메일로 알려주시면 감사하겠습니다. ㅠㅠ
1. 특성이 범주형 자료가 아니고 연속적인 숫자형 자료일 때 임곗값을 구체적으로 정하는 방법?
2. 연속적인 숫자형 자료일 때, 임곗값을 옮기는 step(?)은 어떻게 설정하는지?

이와 같은 방식으로 결정트리는 서브셋의 서브셋을 또 나눕니다. 이 과정에서 max_depth에서 지정한 깊이가 되면 중지하거나 불순도를 줄이는 분할을 찾을 수 없을 때 멈추게 됩니다. 6.7 단원에서 배우는 매개변수도 중지조건에 관여하게 됩니다. 이 모델은 각 단계에서 최적의 분할을 찾기 때문에 현재 단계의 분할이 몇 단계를 거쳐 가장 낮은 불순도로 이어질 수 있을 지는 고려하지 않습니다. 다시 말해, 최적의 솔루션은 보장하지 못합니다.

6.5 Computational Complexity

예측에 필요한 전체 복잡도는 특성 수와 무관하게 매우 좋은 $O(\log_2(m))$입니다.
그러나 훈련 알고리즘은 각 노드에서 모든 훈련 샘플의 모든 특성을 비교하기 때문에, 훈련 복잡도는 $O(n \times m \log(m))$입니다.
- 여기서 $O(m\log(m))$은 데이터들을 정렬하는데 걸리는 계산 복잡도입니다.

6.6 Gini Impurity or Entropy

criterion 매개변수를 ‘entropy’로 지정하면 엔트로피 불순도를 사용할 수 있습니다.

엔트로피 방정식
$H_i = - \sum^n_{k=1 \\ p_{i,k}\neq 0} p_{i,k}\log_2(p_{i,k})$

실제로는 지니 불순도와 큰 차이는 없습니다. 지니 불순도가 조금 더 계산이 빠르지만 지니 불순도는 가장 빈도 높은 클래스를 한쪽 가지로 고립시키는 경향이 있는 반면 엔트로피는 조금 더 균형 잡힌 트리를 만듭니다.

6.7 Regularization Hyperparameters

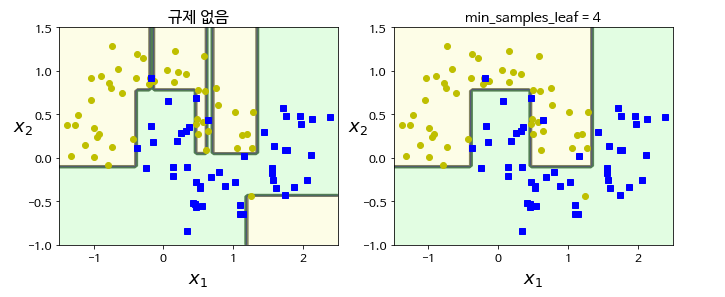
결정트리는 훈련 데이터에 대한 제약사항이 거의 없습니다. 따라서 제한을 따로 두지 않으면 트리가 훈련 데이터에 과대적합되기가 쉽습니다. 이 문제를 트리의 자유도를 제한해서 해결합니다.

min_samples_split - 분할 되기 위해 노드가 가져야 하는 최소 샘플 수를 제한합니다.
min_samples_leaf - 리프 노드가 가지고 있어야 할 최소 샘플 수를 제한합니다.
min_weight_fraction_leaf - 가중치가 부여된 전체 샘플 수에서의 비율(?)을 제한합니다.
max_depth - 트리의 최대 깊이를 제한합니다.
max_leaf_nodes - 리프 노드의 최대 수를 제한합니다.
max_features - 각 노드에서 분할에 사용할 특성의 최대 수를 제한합니다.

from sklearn.datasets import make_moons
Xm, ym = make_moons(n_samples=100, noise=0.25, random_state=53)

deep_tree_clf1 = DecisionTreeClassifier(random_state=42)
deep_tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)
deep_tree_clf1.fit(Xm, ym)
deep_tree_clf2.fit(Xm, ym)

plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(deep_tree_clf1, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("규제 없음", fontsize=16)
plt.subplot(122)
plot_decision_boundary(deep_tree_clf2, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("min_samples_leaf = {}".format(deep_tree_clf2.min_samples_leaf), fontsize=14)

plt.show()

tree3

6.8 Regression

결정트리는 회귀에도 사용할 수 있습니다.

이차함수를 만들어 보겠습니다.

np.random.seed(42)
m = 200
X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10

회귀버전 결정트리를 가져오겠습니다.

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor(max_depth=1, random_state=42)
tree_reg.fit(X, y)

트리를 훈련시키고 그림을 그려보겠습니다.

tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)

def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
    x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
    y_pred = tree_reg.predict(x1)
    plt.axis(axes)
    plt.xlabel("$x_1$", fontsize=18)
    if ylabel:
        plt.ylabel(ylabel, fontsize=18, rotation=0)
    plt.plot(X, y, "b.")
    plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")

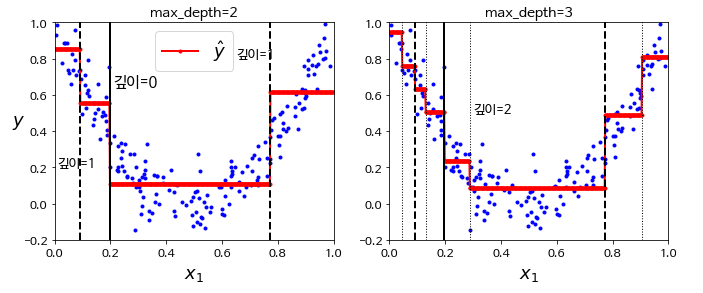
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_regression_predictions(tree_reg1, X, y)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
    plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "깊이=0", fontsize=15)
plt.text(0.01, 0.2, "깊이=1", fontsize=13)
plt.text(0.65, 0.8, "깊이=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)

plt.subplot(122)
plot_regression_predictions(tree_reg2, X, y, ylabel=None)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
    plt.plot([split, split], [-0.2, 1], style, linewidth=2)
for split in (0.0458, 0.1298, 0.2873, 0.9040):
    plt.plot([split, split], [-0.2, 1], "k:", linewidth=1)
plt.text(0.3, 0.5, "깊이=2", fontsize=13)
plt.title("max_depth=3", fontsize=14)

plt.show()

tree4

결정트리가 어떤 방식으로 판단했는지 살펴보겠습니다.

def export_graphviz_k2h(ML_algorithms, image_path_k2h=IMAGE_PATH):
    if not os.path.isdir(image_path_k2h):#github 코드로는 작동이 안되서
        os.makedirs(image_path_k2h) ##직접 image 폴더, decision_trees 폴더를 만듦
    export_graphviz(
    ML_algorithms,
    out_file=image_path("regression_tree.dot"), ##C:\Python\image\decisiontrees\iris_tree.dot
    feature_names=["x1"],
    rounded=True, ##박스 생김새
    filled=True ##박스 생김새
        )

export_graphviz_k2h(tree_reg) ##dot 파일을 만들어줌

import graphviz
with open("images/decision_trees/regression_tree.dot") as f:
    dot_graph = f.read()

dot = graphviz.Source(dot_graph)
dot.format = 'png'
dot.render(filename='regression_tree', directory='images/decision_trees', cleanup=True)
dot ##시스템 변수, PATH에 graphviz가 있어야함

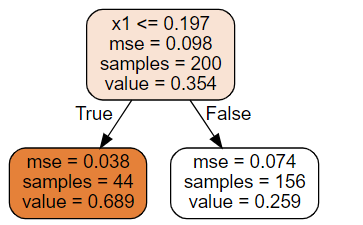
tree5

앞서 만든 분류 트리와 비슷해 보이지만, 주요한 차이는 각 노드에서 클래스를 예측하는 대신 어떤 값을 예측한다는 것입니다. 만약 $x_1$ = 0.6인 샘플을 넣게 되면, value=0.259인 leaf node에 도달하게 됩니다. leaf node에 있는 156개 훈련 샘플의 평균 타깃값으로 테스트 샘플의 값이 예측됩니다. 이 예측값을 사용해 156개 샘플에 대한 평균제곱오차(MSE)를 계산하면 0.074가 됩니다.

회귀를 위한 CART 비용함수
$J(k,t_k) = \frac{m_{left}}{m}MSE_{left} + \frac{m_{right}}{m}MSE_{right} \\$ $\text{where}\ \ MSE_{node} = \sum_{i \in node} (\hat{y}_{node} - y^{(i)})^2 \\ \hat{y}_{node} = \frac{1}{m_{node}} \sum_{i \in node}y^{(i)}$

회귀 작업에서도 결정트리가 과대적합되기 쉬우니 유의해야 합니다.

6.9 Instability

결정 트리는 이해하고 해석하기 쉽고, 사용하기 편하고, 여러 용도로 사용할 수 있으며, 성능도 뛰어납니다. 하지만 결정 트리는 계단 모향의 결정 경계를 만듭니다. 다시 말해, 축에 수직인 경계를 만드는데, 이 때문에 회전에 민감합니다. 이런 문제를 해결하는 한 가지 방법은 훈련 데이터를 더 좋은 방향으로 회전시키는 PCA 기법을 사용하는 것입니다.

또 다른 점은 훈련 데이터에 있는 작은 변화에도 민감하다는 것입니다. 그리고 사이킷런에서 사용하고 있는 훈련 알고리즘은 확률적이기 때문에(각 노드에서 평가할 후보 특성을 무작위로 선택합니다) 같은 훈련 데이터에서도 다른 모델을 얻게 될 수 있습니다. 다음 장에서 보게 될 랜덤 포레스트는 많은 트리에서 만든 예측을 평균하기 때문에 이런 불안정성을 극복할 수 있습니다.

저희는 6단원에서 결정트리 모델의 사용방법과 이론을 배웠습니다. 다음 단원에서는 랜덤 포레스트 모델을 살펴보도록 하겠습니다.