지난 포스트에는 머신러닝 중 한가지인 Decision Tree에 대해서 알아보았습니다.
[쉽게읽는 머신러닝-라온피플] 3. Decision Tree
오늘은 또다른 머신러닝의 모델 중 하나인 Naive Bayes에 대해 알아보는 시간을 가지겠습니다!


그럼, 출발할까요?!

1. Naive Bayes?

‘Bayes Theorem’에 기반한 분류기(Classifier)입니다. ‘Naive’가 붙는 이유는 그것의 가정이 맞을 수도 틀릴 수도 있기 때문입니다.

간단히 말해서, Naive Bayes Classifier는 한 클래스의 특징의 존재가 그 클래스의 다른 특징의 존재와 연관이 안되어있다고 가정합니다. 예를 들면, 만약 빨간색이고, 둥글며, 4인치 둘레인 과일을 사과라고 해보죠. 이 특징들은 서로 어느정도 종속적임에도 불구하고 Naive Bayes Classifier는 이 모든 특징들이 일어날 확률을 전부 독립이라고 가정합니다.

이 때문에 ‘Simple Bayes’나 ‘Idiot Bayes’ (단순, 멍청…) 라고도 불립니다. 특징이 많을때 ‘단순화’ 시켜 빠르게 판단을 내릴 때 주로 사용됩니다.
(예, 문서 분류, 질병 진단, 스팸 메일 분류 등)

2. Bayes Theorem에서 유도

• P(c|x) :
  특정 개체 x가 특정 그룹 c에 속할 사후 확률(Posterior Probability)이며 Naive Bayes를 통해 구하고자 하는 것
• P(c|x) :
  특정 그룹 c인 경우에 특정 개체 x가 거기에 속할 조건부 확률, 가능성(Likelihood)
• P(c) :
  특정 그룹 c가 발생할 빈도, 즉 클래스 사전 고유 확률(Class Prior Probability)
• P(x) :
  특정 개체x가 발생할 확률(Predictor 사전확률)이며, 모든 그룹에 대해 동일하기 때문에 보통 이 항목은 무시됨
  

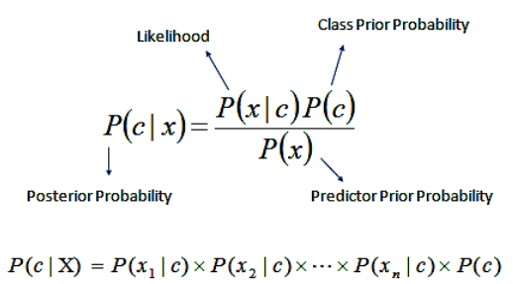
중요한 부분은 특정 개체x를 규정짓는 특징들(x₁, … ,x_n)이 서로 독립적이라면, P(x|c)는 위 식처럼 각각의 특징들이 발생할 확률의 곱으로 쉽게 표현할 수 있습니다.

3. Naive Bayes의 예

‘Drew’라는 이름을 갖는 사람이 많이 있는 경우를 생각해보죠. 아래 그림처럼 ‘Drew’는 여자일수도, 남자일수도 있습니다. ‘Drew’라는 이름을 가진 남자 그룹을 c₁, 여자그룹을 c₂라고 하죠.

그럼 ‘Drew’라는 사람이 c₁에 속할 확률은 어떻게 될까요?

바로 아래 식처럼 됩니다.

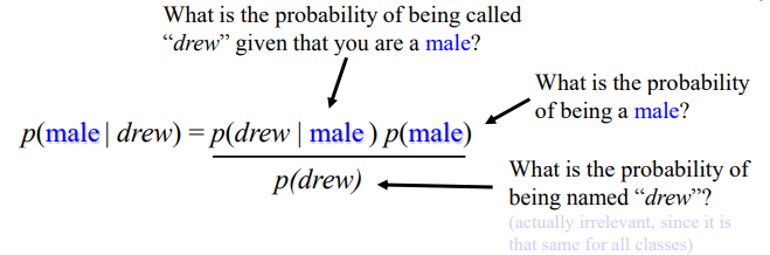
(P(male|drew) : ‘Drew’의 이름을 가진 사람이 남자일 확률
P(drew|male) : 남자가 ‘Drew’의 이름을 가질 확률
P(male) : 남자일 확률
P(drew) : 이름이 ‘Drew’일 확률)

여기서, 한 경잘서에 있는 경찰관의 이름이 아래 표로 주어졌을 때, ‘Drew’라는 이름의 사람이 남자인지 여자인지 판별해봅시다!

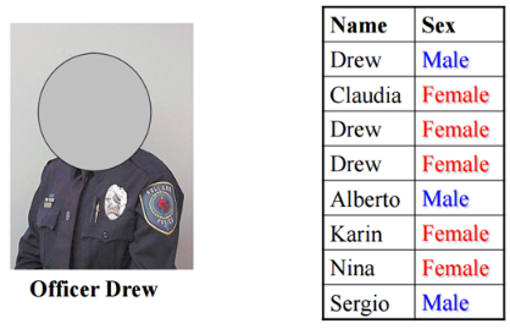
이 문제를 풀려면, P(male|drew)와 P(female|drew)을 구해 큰 쪽을 선택합니다.

Bayes 식에 따라 계산을 하면,

따라서, ‘Drew’라는 이름을 쓰는 경찰관은 여성일 확률이 높다는 것을 알 수 있습니다!

4. Naive Bayes의 장단점

• 장점
  • 그룹이 여러 개 있는 multi-class 분류에서 특히 쉽고 빠르게 예측이 가능
  • 독립이라는 가정이 유효하면, logistic regression과 같은 다른 방식에 비해 훨씬 결과가 좋고, 학습데이터도 적게 필요
  • 수치형 데이터보다 범주형 데이터(categorical data)에 특히 효과적
    
    
• 단점
  • 학습데이터에는 없고 검사데이터에만 있는 범주(category)에선 확률이 0이 되어 정상적 예측이 불가(‘zero frequency’라고 부름) 이를 피하기 위해서 smoothing technique이 필요(Laplace 추정이 대표적 기법)
  • 독립이 라는 가정이 성립되지 않거나 약한 경우 신뢰도가 떨어짐
  • 현실에는 완전히 독립적인 상황이 많지 않음

출처 :
쉽게 읽는 머신 러닝 - 라온피플
stackoverflow
www.cs.ucr.edu