지난 포스트에는 머신러닝 중 한가지인 Naive Bayes에 대해서 알아보았습니다.
[쉽게읽는 머신러닝-라온피플] 4. Naive Bayes
오늘은 또다른 머신러닝의 강력한 모델 중 하나인 Support Vector Machine(SVM)에 대해 알아보는 시간을 가지겠습니다!
가즈아ㅏㅏㅏ!
Vladimir N. Vapnik과 Alexey Ya. Chervonekis에 의해 개발되었습니다.
인공 신경망에 비해 간결하고 뛰어난 성능을 보여서 90년대 들어 각광을 받았습니다.
Support Vector와 Hyper-plane이 주요 개념인 Machine Learning Algorithm 중 하나이며, 지도 학습 모델입니다.
분류(classification)나 회귀분석(regression)에 사용이 가능합니다.
Hyper-plane을 이용해 카테고리를 나눕니다.
주어진 데이터 집합을 바탕으로 새로운 데이터가 어느 집합에 속할지 판단하는 비확률적 이진 선형 분류모델을 만듭니다.
데이터가 사상된 공간에서 분류모델은 경계로 표현이 되는데 SVM알고리즘은 그 중 가장 폭(Margin)이 큰 경계를 찾는 알고리즘입니다.
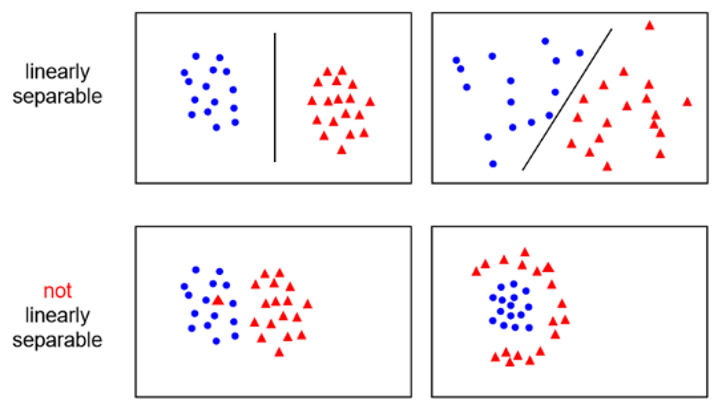
위 그림에서 알 수 있듯이, 데이터를 선형적으로 구분이 가능한 것을 Linearly separable 하다고 합니다.
아래 그림에서 어느것이 가장 분류가 잘 되어 보이나요?
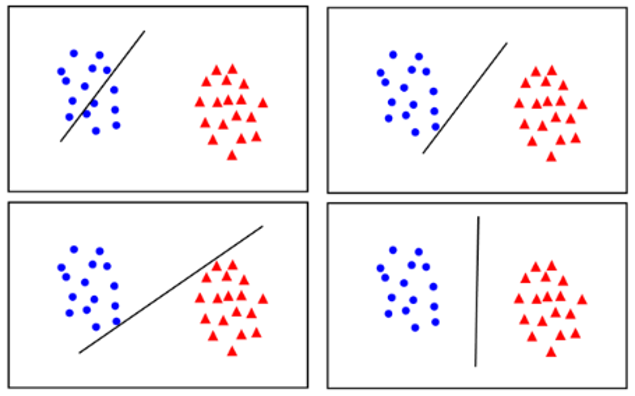
네! 오른쪽 아래 그림입니다. 경계선을 기준으로 데이터 까지의 거리가 가장 멀리 적절하게 떨어져 있기 때문이죠.
SVM은 이런 최대의 Margin을 가진 경계를 구합니다. 그렇게 해야 새로운 데이터가 들어와도 잘 분류할 가능성이 커지기 때문이죠.
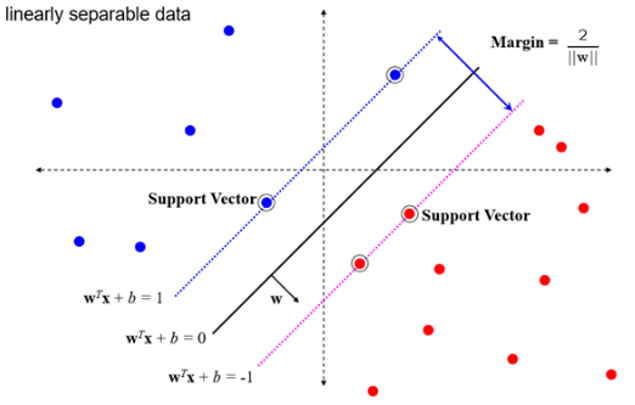
마진의 폭은 \(2/(‖𝑤‖)\) 입니다.
즉, 마진의 폭이 최대가 되게 하려면 ‖𝑤‖가 최소가 되어야 합니다.
‖𝑤‖ 최소 -> ‖𝑤‖2 최소-> quadratic optimization(최적화 방법)
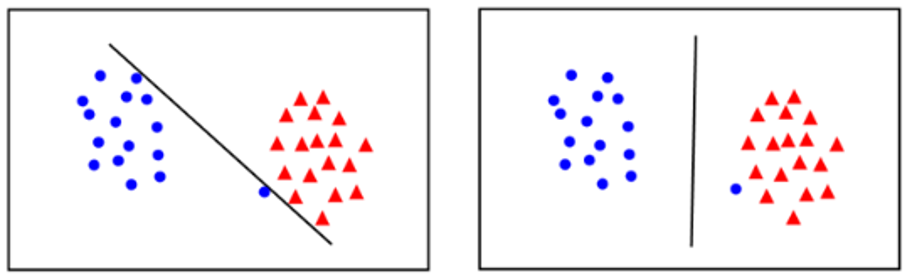
좌측의 그림은 Margin이 거의 없습니다. 하지만 새로운 데이터가 들어올 경우 에러가 발생할 가능성이 높죠.
우즉은 오류는 있지만 Margin이 큽니다. 새로운 데이터가 들어왔을 떄 예측을 더 잘 할수 있습니다.
간단한 함수로 대충 데이터를 뽑아 Machine을 학습시키면 학습이 어렵거나 Overfitting이 발생할 수 있는데 이것을 피하기 위해서 고안된 개념입니다.
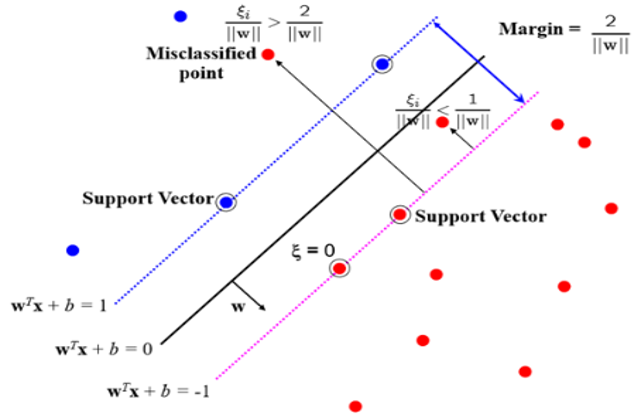
(Slack = 0 : 정상,
0 < Slack < 1 : Margin violation
Slack > 1 : 분류가 잘못됨)
SVM 최적화 (2/‖𝑤‖ 의 최대화)를 수행할 때 Slack 까지 고려하면 아래식으로 표현이 가능합니다.
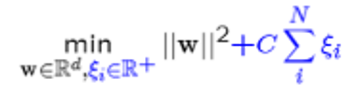
(Regularization(파란색 부분) : Overfitting을 막기위한 Penalty 항)
C(Regularization Parameter)값이 크면 허용오차의 개수가 작아야 하기 때문에 Margin이 좁아집니다. C값이 무한대로 가게 되면 학습오차가 생기면 안됩니다. 반대로 C값이 작아지면 Margin이 커집니다
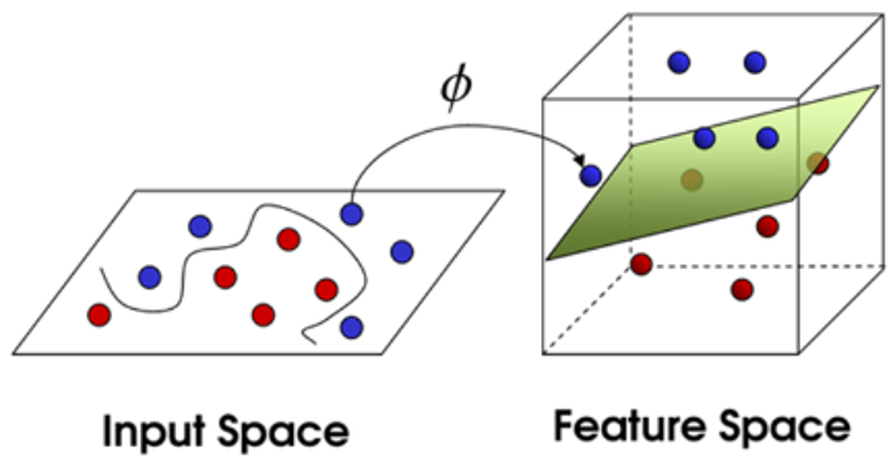
데이터를 변환 (Transform, Mapping) 해서 새로운 공간에서 Hyper-plane으로 나누고 구분을 합니다.
Kernel Trick은 저차원에서는 선형적으로 구별이 불가능한 Data set을 고차원으로 Mapping(특정 함수를 통해 변환)을 한 후 선형적으로 구별하는 방법입니다. 이때 쓰이는 함수를 Kernel function이라고 합니다.
(여러가지 Kernel function이 있으나 추후에 Hands-on Machine Learning책을 정리할때 좀더 자세히 다루겠습니다.)
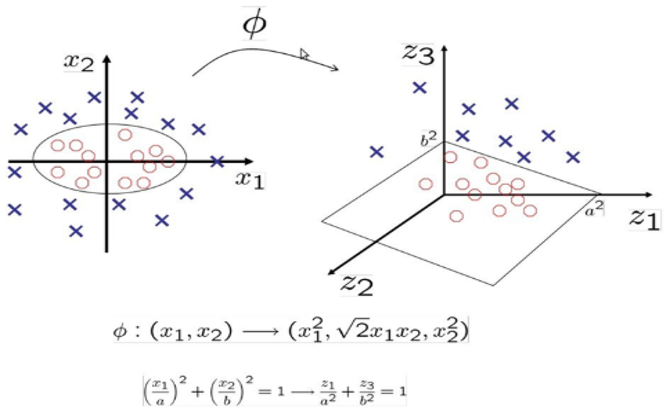
사실 차원을 옮기지 않아도 비선형적으로 구분을 할 수 있습니다. (그림 좌측에서 타원으로 구분) 그럼에도 불구하고 Kernel trick을 쓰는 이유는 간결하게 표현이 가능하기 때문입니다.
또한 계산의 복잡가 입력공간의 차원수에 영향을 받지 안습니다. 즉, 고차원으로 올라가도, 계산 속도가 크게 차이가 나지 않는 다는 뜻이죠.